
| A. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | B. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$| | C. | |$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|-|$\overrightarrow{a}$| | D. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
分析 由已知可得$\overrightarrow{a}$•$\overrightarrow{b}$=-|$\overrightarrow{a}$||$\overrightarrow{b}$|,进而可得|$\overrightarrow{a}$+$\overrightarrow{b}$|2=(|$\overrightarrow{a}$|-|$\overrightarrow{b}$|)2,进而得到答案.
解答 解:∵|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,那么$\overrightarrow{a}$与$\overrightarrow{b}$反向,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-|$\overrightarrow{a}$||$\overrightarrow{b}$|,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=($\overrightarrow{a}$+$\overrightarrow{b}$)2=$\overrightarrow{a}$2+2$\overrightarrow{a}$•$\overrightarrow{b}$+$\overrightarrow{b}$2=|$\overrightarrow{a}$|2-2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|+|$\overrightarrow{b}$|2=(|$\overrightarrow{a}$|-|$\overrightarrow{b}$|)2,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|,
故选:A
点评 本题考查的知识点是向量的模,向量的数量积,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设函数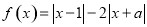 .
.
(1)当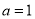 时,求不等式
时,求不等式 的解集;
的解集;
(2)若不等式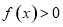 ,在
,在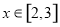 上恒成立,求
上恒成立,求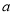 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com