
分析 根据向量的坐标运算和向量的模的计算以及向量的平行和垂直的条件即可求出.
解答 解:(1)设$\overrightarrow{a}$=(x,y),
∵|$\overrightarrow{a}$|=2$\sqrt{3}$,
∴x2+y2=12,
∵$\overrightarrow{b}$=(-1,3),$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴3x=-y,
解得x=$\frac{\sqrt{30}}{5}$,y=-$\frac{3\sqrt{30}}{5}$,或x=-$\frac{\sqrt{30}}{5}$,y=$\frac{3\sqrt{30}}{5}$,
∴$\overrightarrow{a}$=($\frac{\sqrt{30}}{5}$,-$\frac{3\sqrt{30}}{5}$),或(-$\frac{\sqrt{30}}{5}$,$\frac{3\sqrt{30}}{5}$),
(2)∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴-x+3y=0,
∵x2+y2=12,
∴y=$\frac{\sqrt{30}}{5}$,x=$\frac{3\sqrt{30}}{5}$,或y=-$\frac{\sqrt{30}}{5}$,x=-$\frac{3\sqrt{30}}{5}$,
∴$\overrightarrow{a}$=(-$\frac{3\sqrt{30}}{5}$,-$\frac{\sqrt{30}}{5}$),或($\frac{3\sqrt{30}}{5}$,$\frac{\sqrt{30}}{5}$).
点评 本题考查了向量的坐标运算和向量的模的计算以及向量的平行和垂直的条件,属于基础题.


科目:高中数学 来源: 题型:填空题
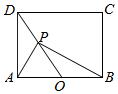 如图在长方形ABCD中,$AB=2\sqrt{2}$,AD=2,O为AB的中点,若P是线段DO上动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PD}$的最小值是-3.
如图在长方形ABCD中,$AB=2\sqrt{2}$,AD=2,O为AB的中点,若P是线段DO上动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PD}$的最小值是-3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
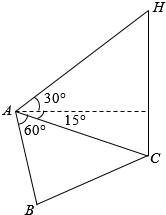 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com