
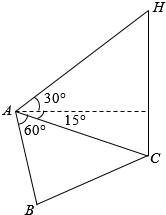
 Ϊ��Ӧ���������ص��������⣬ij�����������е�λ�о���һ���µĵ��������������������������Ե��䵽���н�������۲⣮��ͼ��ʾ����������������C�ؽ��е���ʵ�飬��A��B���ؽ��й۲쵯��Ч������֪A��B�������100�ף���BAC=60����A����������������ʱ���B����$\frac{2}{17}$�루��֪�����ڸõصĴ����ٶ�Ϊ340��/�룩����A�ز�ø�������C��ʱ�ĸ���Ϊ15�㣬A�ز�ø���������ߵ�H��������Ϊ30�㣮
Ϊ��Ӧ���������ص��������⣬ij�����������е�λ�о���һ���µĵ��������������������������Ե��䵽���н�������۲⣮��ͼ��ʾ����������������C�ؽ��е���ʵ�飬��A��B���ؽ��й۲쵯��Ч������֪A��B�������100�ף���BAC=60����A����������������ʱ���B����$\frac{2}{17}$�루��֪�����ڸõصĴ����ٶ�Ϊ340��/�룩����A�ز�ø�������C��ʱ�ĸ���Ϊ15�㣬A�ز�ø���������ߵ�H��������Ϊ30�㣮���� ��1���ڡ�ABC��ʹ�����Ҷ����з��̽����
��2���ڡ�ACH��ʹ�����Ҷ��������
��� �⣺��1������A����������������ʱ���B����$\frac{2}{17}$�룬
��AC-BC=340��$\frac{2}{17}$=40����BC=AC-40��
�ڡ�ABC�У������Ҷ�����BC2=AB2+AC2-2AB��AC��cos��BAC��
�ࣨAC-40��2=1002+AC2-100AC�����AC=420��
��2���������֪��H=60�㣬��HAC=45�㣬
�ڡ�ACH�У������Ҷ�����$\frac{AC}{sinH}=\frac{CH}{sin��CAH}$��
��CH=$\frac{ACsin��CAH}{sinH}$=$\frac{420��\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=140$\sqrt{6}$��
���� ���⿼���������Ҷ������������ε�ʵ��Ӧ�ã����ڻ����⣮


 ��һ����ͬ���ɽ�����ϵ�д�
��һ����ͬ���ɽ�����ϵ�д� ������Ӧ���ϵ�д�
������Ӧ���ϵ�д� ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
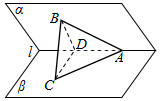 ��ͼ��ʾ������Ǧ�-l-�µ��������һ��ֱ��AB��������l�ļн�Ϊ45�㣮AB��ƽ������ɵĽ�Ϊ30�㣮���������ǵĴ�С��
��ͼ��ʾ������Ǧ�-l-�µ��������һ��ֱ��AB��������l�ļн�Ϊ45�㣮AB��ƽ������ɵĽ�Ϊ30�㣮���������ǵĴ�С���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
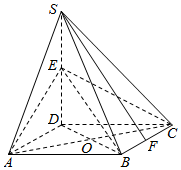 ��ͼ������S-ABCD�����������Σ�SD��ƽ��ABCD��SD=AD=2����E��SD���е㣬F��BC�߶��ϵĵ㣬O��AC��BD�Ľ��㣮
��ͼ������S-ABCD�����������Σ�SD��ƽ��ABCD��SD=AD=2����E��SD���е㣬F��BC�߶��ϵĵ㣬O��AC��BD�Ľ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{5}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com