
分析 求函数的导数,利用函数的单调性和导数之间的关系求出函数的最值即可.
解答 解:函数的导数f′(x)=$\frac{{x}^{2}+1-(x-1)•2x}{({x}^{2}+1)^{2}}$=$\frac{-({x}^{2}-2x-1)}{({x}^{2}+1)^{2}}$,
由f′(x)=0得,x2-2x-1=0,即x=$\frac{2+2\sqrt{2}}{2}$=1+$\sqrt{2}$,或x=1-$\sqrt{2}$,
又x∈[0,4],当x∈[0,1+$\sqrt{2}$)时,f′(x)>0,
当x∈(1+$\sqrt{2}$,4]时,f′(x)<0,
即当x=1+$\sqrt{2}$时,函数取得极大值同时也是最大值f(1+$\sqrt{2}$)=$\frac{1+\sqrt{2}-1}{(1+\sqrt{2})^{2}+1}$=$\frac{\sqrt{2}}{4+2\sqrt{2}}$=$\frac{\sqrt{2}-1}{2}$,
∵f(0)=-1,f(4)=$\frac{4-1}{16+1}$=$\frac{3}{17}$,
∴f(0)<f(4),
即函数的最小值为-1,
故函数的最小值是-1,最大值是$\frac{\sqrt{2}-1}{2}$.
点评 本题主要考查函数最值的求解,求函数的导数,利用导数研究函数的最值是解决本题的关键,综合性较强,运算量较大.


科目:高中数学 来源: 题型:填空题
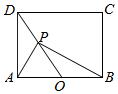 如图在长方形ABCD中,$AB=2\sqrt{2}$,AD=2,O为AB的中点,若P是线段DO上动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PD}$的最小值是-3.
如图在长方形ABCD中,$AB=2\sqrt{2}$,AD=2,O为AB的中点,若P是线段DO上动点,则($\overrightarrow{PA}$+$\overrightarrow{PB}$)•$\overrightarrow{PD}$的最小值是-3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ln|x| | B. | y=$\sqrt{{x}^{2}-1}$ | C. | y=sinx | D. | y=cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
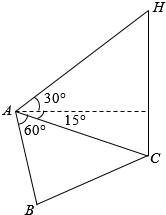 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com