
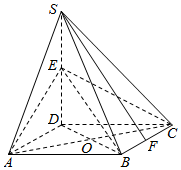
 如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.
如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.分析 (1)线面平行的判定定理即可得到结论.
(2)建立空间直角坐标系,求出对应平面的法向量,利用向量法进行求解即可.
解答 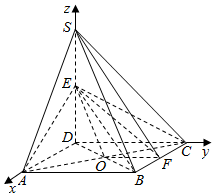 证明:(Ⅰ)连接OE,
证明:(Ⅰ)连接OE,
则O是BD的中点,
∵E是SD的中点,
∴OE是△BDS的中位线,
∴OE∥SB,
∵OE?平面SBC,SB?平面SBC,
∴OE∥平面SBC;
(Ⅱ)∵四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,
∴建立以D为坐标原点的空间直角坐标系如图:
若F为BC的中点,
则C(0,2,0),A(2,0,0),O(1,1,0),S(0,0,2),E(0,0,1),B(2,2,0),F(1,2,0),
则$\overrightarrow{OE}$=(-1,-1,1),$\overrightarrow{OF}$=(0,1,0),$\overrightarrow{OC}$=(-1,1,0),
设COE的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{OE}=0}\\{\overrightarrow{m}•\overrightarrow{OC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-x-y+z=0}\\{-x+y=0}\end{array}\right.$,
令y=1,则x=1,z=2,即$\overrightarrow{m}$=(1,1,2),
设OEF的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{OE}=-x-y+z=0}\\{\overrightarrow{n}•\overrightarrow{OF}=y=0}\end{array}\right.$,令x=1,则y=0,z=1,即$\overrightarrow{n}$=(1,0,1),
cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1+2}{\sqrt{6}•\sqrt{2}}$=$\frac{\sqrt{3}}{2}$,
∴<$\overrightarrow{m}$,$\overrightarrow{n}$>=30°,
∵二面角C-OE-F是锐二面角,
∴二面角C-OE-F的大小为30°.
点评 本题主要考查线面平行的判断以及二面角的求解,根据线面垂直的性质定理以及建立坐标系,利用向量法求二面角是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
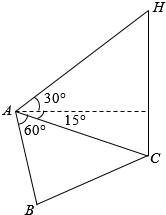 为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.
为了应对日益严重的气候问题,某气象仪器科研单位研究出一种新的弹射型气象仪器,这种仪器可以弹射到空中进行气象观测.如图所示,假设这种仪器在C地进行弹射实验,在A,B两地进行观察弹射效果.已知A、B两地相距100米,∠BAC=60°在A地听到弹射声音的时间比B地晚$\frac{2}{17}$秒(已知声音在该地的传播速度为340米/秒),在A地测得该仪器在C处时的俯角为15°,A地测得该仪器至最高点H处的仰角为30°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com