
分析 由条件可知,方程ax2+bx+2=0的两根为$-\frac{1}{2},\frac{1}{3}$,根据韦达定理即可建立关于a,b的方程组,可解得a=-12,b=-2,从而得到$y=-12(x+\frac{1}{12})^{2}+\frac{25}{12}$,这样即可得出该二次函数在$[-\frac{1}{2},\frac{1}{2}]$上的最大值M和最小值m,从而求出M+m的值.
解答 解:根据题意知,方程ax2+bx+2=0的两根为$-\frac{1}{2},\frac{1}{3}$;
∴$\left\{\begin{array}{l}{-\frac{1}{2}+\frac{1}{3}=-\frac{b}{a}}\\{-\frac{1}{2}•\frac{1}{3}=\frac{2}{a}}\end{array}\right.$;
解得a=-12,b=-2;
∴y=-12x2-2x+2=$-12(x+\frac{1}{12})^{2}+\frac{25}{12}$;
∴$x=-\frac{1}{12}$时,$M=\frac{25}{12}$;$x=\frac{1}{2}$时,m=-2;
∴$M+m=\frac{1}{12}$.
故答案为:$\frac{1}{12}$.
点评 考查一元二次不等式的解集和对应一元二次方程的实数根的关系,韦达定理,以及配方求二次函数最值的方法.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
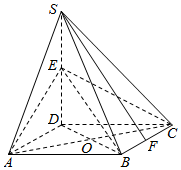 如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.
如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (-∞,-$\sqrt{3}$) | D. | [-2,$-\sqrt{3}$)∪($\sqrt{3}$,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com