
(本题满分14分)如图,已知椭圆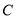 :
: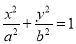 ,其左右焦点为
,其左右焦点为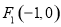 及
及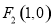 ,过点
,过点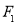 的直线交椭圆
的直线交椭圆 于
于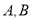 两点,线段
两点,线段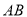 的中点为
的中点为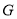 ,
,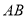 的中垂线与
的中垂线与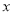 轴和
轴和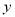 轴分别交于
轴分别交于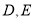 两点,且
两点,且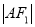 、
、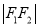 、
、 构成等差数列.
构成等差数列.

(1)求椭圆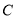 的方程;
的方程;
(2)记△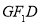 的面积为
的面积为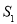 ,△
,△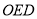 (
(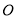 为原点)的面积为
为原点)的面积为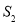 .试问:是否存在直线
.试问:是否存在直线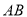 ,使得
,使得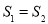 ?说明理由.
?说明理由.
(1)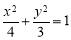 ;(2)不存在直线
;(2)不存在直线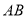 ,使得
,使得  .
.
【解析】
试题分析:(1)求椭圆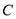 的标准方程,由已知
的标准方程,由已知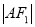 、
、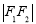 、
、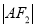 构成等差数列,即
构成等差数列,即 ,由椭圆的定义可得,
,由椭圆的定义可得, ,由已知焦点为
,由已知焦点为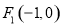 及
及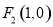 ,可得
,可得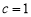 ,可求出
,可求出 ,从而得椭圆
,从而得椭圆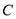 的标准方程;(2)记△
的标准方程;(2)记△ 的面积为
的面积为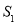 ,△
,△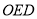 (
(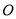 为原点)的面积为
为原点)的面积为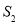 .试问:是否存在直线
.试问:是否存在直线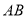 ,使得
,使得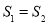 ?说明理由,这是探索性命题,一般假设其存在,本题假设存在直线
?说明理由,这是探索性命题,一般假设其存在,本题假设存在直线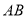 ,使得
,使得  ,由题意直线
,由题意直线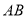 不能与
不能与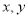 轴垂直,故设
轴垂直,故设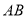 方程为
方程为 ,将其代入
,将其代入 ,整理得
,整理得  ,设
,设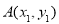 ,
,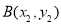 ,由根与系数关系,表示出点
,由根与系数关系,表示出点 的坐标,写出中垂线方程,得点
的坐标,写出中垂线方程,得点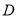 的坐标,由于
的坐标,由于 和
和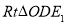 相似,若
相似,若 ,则
,则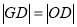 ,建立方程,求解斜率
,建立方程,求解斜率 的值,若有解,则存在,若无解,则不存在.
的值,若有解,则存在,若无解,则不存在.
试题解析:(1)因为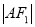 、
、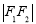 、
、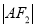 构成等差数列,
构成等差数列,
所以 ,所以
,所以 . (2分)
. (2分)
又因为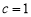 ,所以
,所以 , (3分)
, (3分)
所以椭圆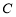 的方程为
的方程为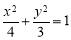 . (4分)
. (4分)
(2)假设存在直线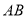 ,使得
,使得  ,显然直线
,显然直线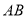 不能与
不能与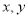 轴垂直.
轴垂直.
设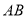 方程为
方程为 (5分)
(5分)
将其代入 ,整理得
,整理得  (6分)
(6分)
设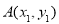 ,
,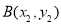 ,所以
,所以 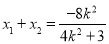 .
.
故点 的横坐标为
的横坐标为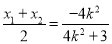 .所以
.所以 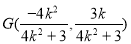 . (8分)
. (8分)
因为  ,所以
,所以  , 解得
, 解得 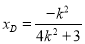 ,
,
即 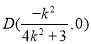 (10分)
(10分)
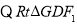 和
和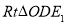 相似,
相似, 若
若 ,则
,则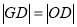 (11分)
(11分)
所以 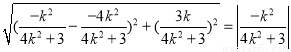 , (12分)
, (12分)
整理得 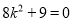 . (13分)
. (13分)
因为此方程无解,所以不存在直线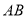 ,使得
,使得  . (14分)
. (14分)
考点:椭圆的方程,直线与二次曲线位置关系.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:选择题
在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务. 已知:①食物投掷地点有远、近两处;②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处.则不同的搜寻方案有( )
A.40种 B.70种 C.80种 D.100种
查看答案和解析>>
科目:高中数学 来源:2015届广东省高三上学期暑假联考文科数学试卷(解析版) 题型:填空题
从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是________.
查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:填空题
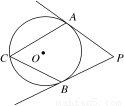
(几何证明选讲)如图所示,⊙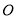 的两条切线
的两条切线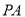 和
和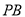 相交于点
相交于点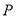 ,与⊙
,与⊙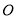 相切于
相切于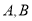 两点,
两点,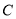 是⊙
是⊙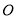 上的一点,若
上的一点,若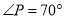 ,则
,则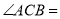 ________.(用角度表示)
________.(用角度表示)
查看答案和解析>>
科目:高中数学 来源:2015届广东省惠州市高三第二次调研考试理科数学试卷(解析版) 题型:选择题
某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么,各班可推选代表人数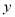 与该班人数
与该班人数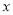 之间的函数关系用取整函数
之间的函数关系用取整函数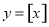 (
(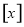 表示不大于
表示不大于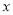 的最大整数)可以表示为( )
的最大整数)可以表示为( )
A.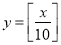 B.
B.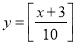 C.
C.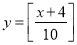 D.
D.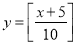
查看答案和解析>>
科目:高中数学 来源:2015届广东省东莞市高二下学期期末理科数学试卷(解析版) 题型:填空题
某班收集了50位同学的身高数据,每一个学生的性别与其身高是否高于或低于中位数的列联表如下:
| 高于中位数 | 低于中位数 | 总计 |
男 | 20 | 7 | 27 |
女 | 10 | 13 | 23 |
总计 | 30 | 20 | 50 |
为了检验性别是否与身高有关系,根据表中的数据,得到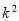 的观测值
的观测值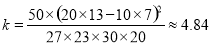 ,
,
因为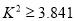 ,所以在犯错误的概率不超过 _________ 的前提下认为性别与身高有关系.
,所以在犯错误的概率不超过 _________ 的前提下认为性别与身高有关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com