
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
分析 根据题意,求出双曲线的焦点坐标以及渐近线方程,由点到直线的距离公式计算可得焦点F到渐近线ay-bx=0的距离为b,结合题意可得b=$\sqrt{3}a$,由双曲线的几何性质可得c=$\sqrt{{a}^{2}+{b}^{2}}$=2a,进而由双曲线离心率公式计算可得答案.
解答 解:根据题意,双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点在x轴上,则其渐近线方程为y=±$\frac{b}{a}$x,即ay±bx=0,
设F(c,0),F到渐近线ay-bx=0的距离d=$\frac{|a×0-b×c|}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{|b×c|}{c}$=b,
又由双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点F到E的渐近线的距离为$\sqrt{3}a$,
则b=$\sqrt{3}a$,
c=$\sqrt{{a}^{2}+{b}^{2}}$=2a,
故双曲线的离心率e=$\frac{c}{a}$=2;
故选:C.
点评 本题考查双曲线的几何性质,注意“双曲线的焦点到其渐近线的距离为b”.


科目:高中数学 来源: 题型:解答题
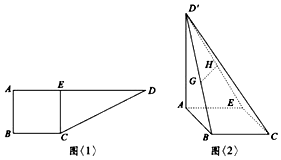 如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.
如图<1>:在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于E点,把△DEC沿CE折到D'EC的位置,使$D'A=2\sqrt{3}$,如图<2>:若G,H分别为D'B,D'E的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
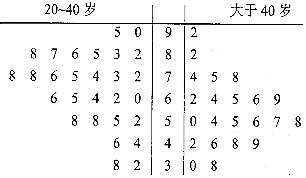 某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.
某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com