
| A. | 3 | B. | -3 | C. | $-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
分析 由题意可得$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{9}{2}$,根据向量的加法的几何意义即可求出答案
解答 解:$|{\overrightarrow{AB}+\overrightarrow{AC}}|=\sqrt{3}|{\overrightarrow{AB}-\overrightarrow{AC}}|$,|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=3
两边平方可得|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2+2$\overrightarrow{AB}$•$\overrightarrow{AC}$=3|$\overrightarrow{AB}$|2+3|$\overrightarrow{AC}$|2-6$\overrightarrow{AB}$•$\overrightarrow{AC}$,
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\frac{9}{2}$,
∴$\overrightarrow{CB}•\overrightarrow{CA}$=($\overrightarrow{CA}$+$\overrightarrow{AB}$)$\overrightarrow{CA}$=${\overrightarrow{CA}}^{2}$+$\overrightarrow{AB}•\overrightarrow{CA}$=${\overrightarrow{CA}}^{2}$-$\overrightarrow{AB}$•$\overrightarrow{AC}$=9-$\frac{9}{2}$=$\frac{9}{2}$,
故选:D.
点评 本题考查了向量的加法的几何意义,以及向量数量积的计算公式,属于基础题


 能力评价系列答案
能力评价系列答案科目:高中数学 来源: 题型:选择题
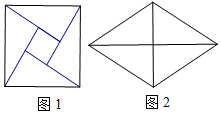 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -$\frac{3}{4}$ | D. | -$\frac{11}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 等腰梯形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com