
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $±\frac{3}{5}$ |
分析 由条件利用同角三角的基本关系,三角函数在各个象限中的符号,求得$cos(\frac{π}{3}+α)$的值.
解答 解:∵α是第二象限角,$tan(\frac{π}{3}+α)=\frac{4}{3}$=$\frac{sin(\frac{π}{3}+α)}{cos(\frac{π}{3}+α)}$,∴$\frac{π}{3}$+α为第三项象限角.
∵${sin}^{2}(\frac{π}{3}+α)$+${cos}^{2}(\frac{π}{3}+α)$=1,sin($\frac{π}{3}+α$)<0,cos($\frac{π}{3}+α$)<0,
求得 $cos(\frac{π}{3}+α)$=-$\frac{3}{5}$,
故选:A.
点评 本题主要考查同角三角的基本关系,三角函数在各个象限中的符号,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | b<c<a | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2>b2 | B. | $\frac{a}{b}>1$ | C. | 2a>2b | D. | lg(a-b)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
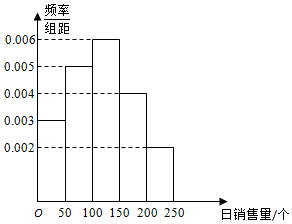 如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为9.
如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为9.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com