
���� ��I���衰����һ����Ŀ����1�֡�Ϊ�¼�A�����¼�A�������ҽ�������������Ȩ���Ի�����������Ȩ����������������뻥���¼��ĸ��ʼ��㹫ʽ���ɵó���
��II���ڽ������ı����У��ĵ÷�Ϊ��ȡֵΪ0��1��2��3��P����=0��=$��1-\frac{2}{3}��^{2}$��P����=1��=${∁}_{2}^{1}•\frac{2}{3}$��$��1-\frac{2}{3}��$��$��1-\frac{2}{3}��$��P����=2��=${∁}_{3}^{2}$$��\frac{2}{3}��^{2}$��$��1-\frac{2}{3}��^{2}$��P����=3��=1-P����=0��-P����=1��-P����=2����
��� �⣺��I���衰����һ����Ŀ����1�֡�Ϊ�¼�A�����¼�A�������ҽ�������������Ȩ���Ի�����������Ȩ��������P��A��=$\frac{1}{2}��\frac{3}{4}$+$\frac{1}{2}����1-\frac{5}{12}��$=$\frac{2}{3}$��
��II���ڽ������ı����У��ĵ÷�Ϊ��ȡֵΪ0��1��2��3��
P����=0��=$��1-\frac{2}{3}��^{2}$=$\frac{1}{9}$��P����=1��=${∁}_{2}^{1}•\frac{2}{3}$��$��1-\frac{2}{3}��$��$��1-\frac{2}{3}��$=$\frac{4}{27}$��P����=2��=${∁}_{3}^{2}$$��\frac{2}{3}��^{2}$��$��1-\frac{2}{3}��^{2}$=$\frac{4}{27}$��P����=3��=1-$\frac{1}{9}$-$\frac{4}{27}$-$\frac{4}{27}$=$\frac{16}{27}$��
��εķֲ��У�
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{1}{9}$ | $\frac{4}{27}$ | $\frac{4}{27}$ | $\frac{16}{27}$ |
���� ���⿼����������뻥���¼��ĸ��ʼ��㹫ʽ����������ķֲ�������ѧ������������������������������������е��⣮


 ����һ������ܼƻ�ϵ�д�
����һ������ܼƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | l�Φ� | B�� | l������� | C�� | l����ཻ | D�� | l���û�й����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
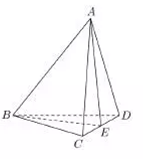 ��ͼ������A-BCD�У���BCDΪ�ȱ������Σ�AC=AD��EΪCD���е㣻
��ͼ������A-BCD�У���BCDΪ�ȱ������Σ�AC=AD��EΪCD���е㣻�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
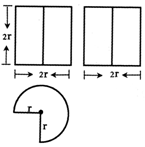
| A�� | 18��+16 | B�� | 20��+16 | C�� | 22��+16 | D�� | 24��+16 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com