
分析 (1)数列{an}满足an>0,4(n+1)an2-nan+12=0,化为:$\frac{{a}_{n+1}}{\sqrt{n+1}}$=2×$\frac{{a}_{n}}{\sqrt{n}}$,即可证明.
(2)由(1)可得:$\frac{{a}_{n}}{\sqrt{n}}$=${a}_{1}×{2}^{n-1}$,可得${a}_{n}^{2}$=n${a}_{1}^{2}$•4n-1.数列{bn}满足bn=$\frac{{{a}_{n}}^{2}}{{t}^{n}}$,可得b1,b2,b3,利用数列{bn}是等差数列即可得出t.
(3)根据(2)的结果分情况讨论t的值,化简8a12Sn-a14n2=16bm,即可得出a1.
解答 (1)证明:数列{an}满足an>0,4(n+1)an2-nan+12=0,
∴$2\sqrt{n+1}{a}_{n}$=$\sqrt{n}$an+1,即$\frac{{a}_{n+1}}{\sqrt{n+1}}$=2$\frac{{a}_{n}}{\sqrt{n}}$,
∴数列{$\frac{{a}_{n}}{\sqrt{n}}$}是以a1为首项,以2为公比的等比数列.
(2)解:由(1)可得:$\frac{{a}_{n}}{\sqrt{n}}$=${a}_{1}×{2}^{n-1}$,∴${a}_{n}^{2}$=n${a}_{1}^{2}$•4n-1.
∵bn=$\frac{{{a}_{n}}^{2}}{{t}^{n}}$,∴b1=$\frac{{a}_{1}^{2}}{t}$,b2=$\frac{{a}_{2}^{2}}{{t}^{2}}$,b3=$\frac{{a}_{3}^{2}}{{t}^{3}}$,
∵数列{bn}是等差数列,∴2×$\frac{{a}_{2}^{2}}{{t}^{2}}$=$\frac{{a}_{1}^{2}}{t}$+$\frac{{a}_{3}^{2}}{{t}^{3}}$,
∴$\frac{2×2{a}_{1}^{2}×4}{t}$=${a}_{1}^{2}$+$\frac{3{a}_{1}^{2}×{4}^{2}}{{t}^{2}}$,
化为:16t=t2+48,解得t=12或4.
(3)解:数列{bn}是等差数列,由(2)可得:t=12或4.
①t=12时,bn=$\frac{n{a}_{1}^{2}•{4}^{n-1}}{1{2}^{n}}$=$\frac{n{a}_{1}^{2}}{4×{3}^{n}}$,Sn=$\frac{n(\frac{{a}_{1}^{2}}{12}+\frac{n{a}_{1}^{2}}{4×{3}^{n}})}{2}$,
∵对任意的n∈N*,均存在m∈N*,使得8a12Sn-a14n2=16bm成立,
∴$8{a}_{1}^{2}$×$\frac{n(\frac{{a}_{1}^{2}}{12}+\frac{n{a}_{1}^{2}}{4×{3}^{n}})}{2}$-a14n2=16×$\frac{m{a}_{1}^{2}}{4×{3}^{m}}$,
∴${a}_{1}^{2}$$(\frac{n}{3}+\frac{{n}^{2}}{{3}^{n}}-{n}^{2})$=$\frac{4m}{{3}^{m}}$,n=1时,化为:-$\frac{1}{3}{a}_{1}^{2}$=$\frac{4m}{{3}^{m}}$>0,无解,舍去.
②t=4时,bn=$\frac{n{a}_{1}^{2}•{4}^{n-1}}{{4}^{n}}$=$\frac{n{a}_{1}^{2}}{4}$,Sn=$\frac{n(\frac{{a}_{1}^{2}}{4}+\frac{n{a}_{1}^{2}}{4})}{2}$,
对任意的n∈N*,均存在m∈N*,使得8a12Sn-a14n2=16bm成立,
∴$8{a}_{1}^{2}$×$\frac{n(\frac{{a}_{1}^{2}}{4}+\frac{n{a}_{1}^{2}}{4})}{2}$-a14n2=16×$\frac{m{a}_{1}^{2}}{4}$,
∴n${a}_{1}^{2}$=4m,
∴a1=$2\sqrt{\frac{m}{n}}$.∵a1为正整数,∴$\sqrt{\frac{m}{n}}$=$\frac{1}{2}$k,k∈N*.
∴满足条件的所有整数a1的值为{a1|a1=2$\sqrt{\frac{m}{n}}$,n∈N*,m∈N*,且$\sqrt{\frac{m}{n}}$=$\frac{1}{2}$k,k∈N*}.
点评 本题考查了三角函数的诱导公式、等比数列的通项公式与求和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,点P为椭圆C上任意一点,且|PF|的最小值为$\sqrt{2}$-1,离心率为$\frac{\sqrt{2}}{2}$,直线l与椭圆C交于不同两点A、B(A、B都在x轴上方),且∠OFA+∠OFB=180°.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F,点P为椭圆C上任意一点,且|PF|的最小值为$\sqrt{2}$-1,离心率为$\frac{\sqrt{2}}{2}$,直线l与椭圆C交于不同两点A、B(A、B都在x轴上方),且∠OFA+∠OFB=180°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
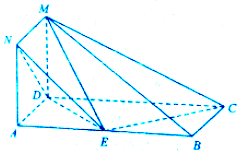 如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.
如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
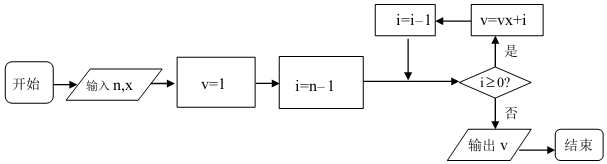
| A. | 130 | B. | 120 | C. | 110 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com