考点:与二面角有关的立体几何综合题,直线与平面平行的判定,点、线、面间的距离计算
专题:空间角
分析:(Ⅰ)连AF、FC
1,由已知条件推导出D为AC
1的中点,取AC的中点E,推导出四边形DEBF是平行四边形,由此能证明DF∥平面ABC.
(Ⅱ)由已知条件推导出FD⊥平面ACC
1,从而得到二面角F-AC
1-C的大小为90°,由此能求出二面角F-AC
1-C的余弦值.
(Ⅲ)由
VF-ACC1=VB-ACC1=
××2=,
VF-ACC1=VC1-ACF=
VC1-ACF=S
△ACF×h,利用等积法能求出点C
1到平面AFC的距离.
解答:
(Ⅰ)证明:连AF、FC
1,
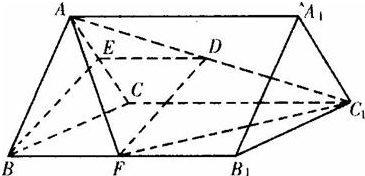
∵三棱柱ABC-A
1B
1C
1是正三棱柱,
且各棱长都等于2,又F为BB
1中点,
∴Rt△ABF≌Rt△C
1B
1F,
∴AF=FC
1.
又在△AFC
1中,FD⊥AC
1,
∴D为AC
1的中点,取AC的中点E,
连接BE及DE,则DE
CC1,
∴DE与FB平行且相等,∴四边形DEBF是平行四边形,
∴FD与BE平行.
∵BE?平面ABC,DF不包含于平面ABC,
∴DF∥平面ABC.
(Ⅱ)解:∵三棱柱ABC-A
1B
1C
1是正三棱柱,
∴ABC是正三角形,BE⊥AC,
∴FD⊥AC,又∵FD⊥AC,∴FD⊥平面ACC
1,
∴二面角F-AC
1-C的大小为90°.
∴二面角F-AC
1-C的余弦值为0.
(Ⅲ)∵AC=2,AF=CF=
,
∴S
△ACF=2,
∴
VF-ACC1=VB-ACC1=
××2=,
VF-ACC1=VC1-ACF=
VC1-ACF=S
△ACF×h,
解得h=
.
∴点C
1到平面AFC的距离为
.
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,考查点到平面的距离的求法,解题时要认真审题,注意等积法的合理运用.

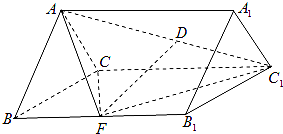 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.
如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
 如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.
如图,在三棱锥P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分别是AB,PB的中点.PC=1,BC=1.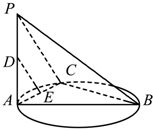 如图,已知AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点,D是线段PA的中点,E是线段AC上的一点.
如图,已知AB是圆的直径,PA垂直圆所在的平面,C是圆上任一点,D是线段PA的中点,E是线段AC上的一点.