
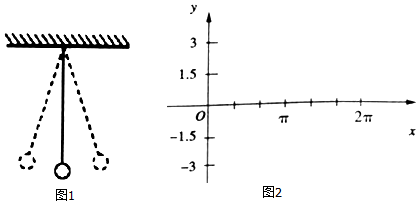
分析 (1)利用函数解析式求解即可.
(2)求出函数的周期,然后求解即可.
(3)画出函数的图象,利用已知条件通过概率转化求解即可.
解答 解:(1)小球摆动时,离开平衡位置的位移s(单位:cm)与时间t(单位:s)的函数关系是:
s=3cos($\sqrt{\frac{g}{l}}$t+$\frac{π}{3}$),t∈[0,+∞),当t=0时,s=3cos$\frac{π}{3}$=$\frac{3}{2}$,
即小球离开平衡位置的位移s是$\frac{3}{2}cm$;
(2)周期$T=\frac{2π}{\sqrt{\frac{g}{l}}}$=2$π\sqrt{\frac{l}{g}}$=$2π\sqrt{\frac{40}{1000}}$=$\frac{2π}{5}$,所以频率$f=\frac{1}{T}=\frac{5}{2π}$,即小球每1s能往复摆动$\frac{5}{2π}$次.
要使小球摆动的周期是1s,即$T=2π\sqrt{\frac{l}{g}}=2π\sqrt{\frac{l}{1000}}=1$,
解得$l=\frac{250}{π^2}$,即线的长度应该调整为$\frac{250}{π^2}cm$.
(3)$f(x)=3cos(x+\frac{π}{3}),x∈[0,2π)$的图象,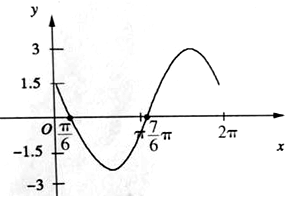
由题意可知,设事件A=“小球离开平衡位置的距离(位移的绝对值)比t=0时小球离开平衡位置的距离小”,只需$|3cos(x+\frac{π}{3})|≤\frac{3}{2}$,解得$0≤x≤\frac{π}{3}$或$π≤x≤\frac{4π}{3}$,由几何概型可知,$P(A)=\frac{{(\frac{π}{3}-0)+(\frac{4π}{3}-π)}}{2π}=\frac{1}{3}$,所以估计符合条件的大约有$300×\frac{1}{3}=100$张.
点评 本题考查三角函数的化简求值,三角函数的图象的应用,概率的求法,考查计算能力.


科目:高中数学 来源: 题型:解答题
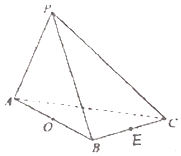 在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.
在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{2}$] | B. | [-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [-$\frac{5}{3}$,+∞) | D. | (-∞,-$\frac{5}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com