
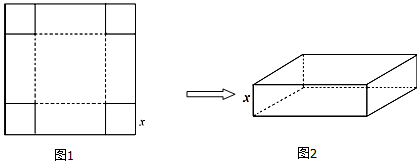
分析 由已知得长方体容积V1=(4-2x)2•x=4(x3-4x2+4x),(0<x<2),求导数,确定函数的单调性,即可得出结论.
解答 解:设切去的正方形边长为x,则焊接成的盒子的底面边长为4-2x,高为x.
所以V1=(4-2x)2•x=4(x3-4x2+4x),(0<x<2)
∴V1′=4(3x2-8x+4).
令V1′=0得x1=$\frac{2}{3}$,x2=2(舍去),
当x<$\frac{2}{3}$时,V1′>0,当$\frac{2}{3}$<x<2时,V1′<0,
∴当x=$\frac{2}{3}$时盒子容积最大,最大容积V1是$\frac{128}{27}$.
点评 本题重点考查利用导数研究函数的性质,利用函数的性质解决不等式、方程问题.重点考查学生的代数推理论证能力.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | $y=±\sqrt{2}x$ | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
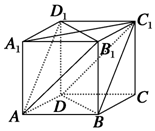 在正方体ABCD-A1B1C1D1中,如图.
在正方体ABCD-A1B1C1D1中,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{26}}}{26}$ | B. | $\frac{{\sqrt{26}}}{12}$ | C. | $\frac{{3\sqrt{26}}}{26}$ | D. | $\frac{{2\sqrt{26}}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com