
分析 (1)运用数列的递推式,可得n≥2时,an=Sn-Sn-1,代入已知,同除以SnSn-1,由等差数列的定义,即可得证;
(2)运用等差数列的通项公式可得$\frac{1}{{S}_{n}}$=2n,求得bn=$\frac{{2}^{n}}{{S}_{n}}$=n•2n+1,运用数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求和.
解答 解:(1)证明:∵-an=2SnSn-1,∴-Sn+Sn-1=2SnSn-1(n≥2)
Sn≠0,∴$\frac{1}{{S}_{n}}$-$\frac{1}{{S}_{n-1}}$=2,又$\frac{1}{{S}_{1}}$=$\frac{1}{{a}_{1}}$=2,
∴{$\frac{1}{{S}_{n}}$}是以2为首项,公差为2的等差数列.
(2)$\frac{1}{{S}_{n}}$=2+2(n-1)=2n,
即有Sn=$\frac{1}{2n}$,
则bn=$\frac{{2}^{n}}{{S}_{n}}$=n•2n+1,
数列{bn}的前n项和Tn=1•22+2•23+…+n•2n+1,
2Tn=1•23+2•24+…+n•2n+2,
两式相减可得,-Tn=22+23+…+2n+1-n•2n+2
=$\frac{4(1-{2}^{n})}{1-2}$-n•2n+2,
化简可得,${T_n}={2^{n+2}}(n-1)+4$.
点评 本题考查等差数列的定义和通项公式的运用,考查数列的递推式,以及数列的求和方法:错位相减法,同时考查等比数列的求和公式,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 选择自然科学类 | 选择社会科学类 | 合计 | |
| 男生 | 60 | 45 | 105 |
| 女生 | 30 | 45 | 75 |
| 合计 | 90 | 90 | 180 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2+x-1≥0 | B. | $?{x_0}∈R,x_0^2+{x_0}-1>0$ | ||
| C. | $?{x_0}∉R,x_0^2+{x_0}-1≥0$ | D. | ?x∉R,x2+x-1>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
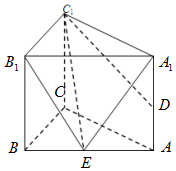 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是AA1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com