
分析 (1)根据销售这种产品所得的年利润=销售所得的收入-销售成本,建立函数关系即可;
(2)利用配方法,求得0<x≤500时,$f(x)=-\frac{1}{200}{(x-450)}^{2}+\frac{1975}{2}$在x=450时取得最大值,x>500时,$f(x)<-\frac{1}{2}×500+1225=975$,即获得的利润最大.
解答 解:(1)当0<x≤500时,$f(x)=5x-\frac{1}{200}{x}^{2}-50•\frac{x}{100}-25$.
当x>500时,$f(x)=5×500-\frac{1}{200}×{500}^{2}-50×\frac{x}{100}-25$,
故$f(x)=\left\{\begin{array}{l}-\frac{1}{200}{x}^{2}+\frac{9x}{2}-250<x≤500\\-\frac{1}{2}x+1225x>500\end{array}\right.$;
(2)当0<x≤500时,$f(x)=-\frac{1}{200}{(x-450)}^{2}+\frac{1975}{2}$
故当x=450时,${f(x)}_{max}=\frac{1975}{2}$;
当x>500时,$f(x)<-\frac{1}{2}×500+1225=975$,
故当该公司的年产量为450件时,当年获得的利润最大.
点评 本题考查了函数模型的性质与运用,考查了简单的建模思想方法,训练里利用配方法求二次函数的最值,是中档题.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{12}$=1 | C. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{10}$=1 | D. | $\frac{{y}^{2}}{10}$-$\frac{{x}^{2}}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}\sqrt{3}$ | B. | $\frac{4}{3}\sqrt{2}$ | C. | $\frac{4}{3}\sqrt{6}$ | D. | $\frac{2}{3}\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
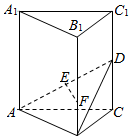 在正三棱柱ABC-A1B1C1中,AB=AA1=1,DC=DC1,AE=ED,F为BB1上任意一点,且FB1=3BF.
在正三棱柱ABC-A1B1C1中,AB=AA1=1,DC=DC1,AE=ED,F为BB1上任意一点,且FB1=3BF.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
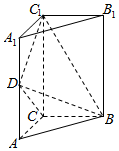 如图,底面是直角三角形的直三棱柱ABC-A1B1C1中,$AC=BC=\frac{1}{2}A{A_1}=1$,D是棱AA1上的动点.
如图,底面是直角三角形的直三棱柱ABC-A1B1C1中,$AC=BC=\frac{1}{2}A{A_1}=1$,D是棱AA1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com