
| A. | $\frac{3}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{3}{2}$ |
分析 利用向量加法的几何意义 得出△ABC是以A为直角的直角三角形.继而求出向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影.
解答 解:∵$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$,
∴($\overrightarrow{AB}$-$\overrightarrow{AO}$)+($\overrightarrow{AC}$-$\overrightarrow{AO}$)=$\overrightarrow{OB}$+$\overrightarrow{OC}$=0,
所以BC为圆O的直径.又|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|=1,
所以∠C=60°,∠B=30°,|$\overrightarrow{BA}$|=$\sqrt{3}$,
所以向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为|$\overrightarrow{BA}$|cosB=$\frac{3}{2}$.
故选:A.
点评 本题考查向量加法的几何意义,向量投影的计算.得出△ABC是以A为直角的直角三角形是关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5,10,15,20,25,30 | B. | 3,13,23,33,43,53 | ||
| C. | 1,2,3,4,5,6 | D. | 2,4,8,16,32,48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
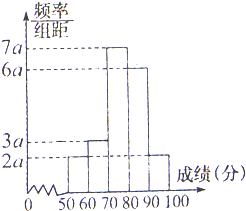 200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:
200名学生,某次数学考试成绩(单位:分)的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,+∞) | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com