
分析 (Ⅰ)求出导函数,根据导函数的意义和切线方程的概念求出参数m,n的值即可;
(Ⅱ)利用作差的方法:A,B关系易判断;
A,C与C,B判断时,作差,构造函数,通过导函数判断函数的单调性,进而得出结论.
解答 解:(Ⅰ)$f'(x)=\frac{m}{x}-\frac{n}{x^2}$.
由于$\left\{\begin{array}{l}f(1)=n=0\\ f'(1)=m-n=1\end{array}\right.$所以m=1,n=0.
(Ⅱ)由(Ⅰ)知f(x)=lnx.
(i)$A-B=ln\frac{a+b}{2}-\frac{lna+lnb}{2}=ln\frac{a+b}{{2\sqrt{ab}}}≥1=0$,
而a≠b,故A>B.
(ii)$A-C=ln\frac{a+b}{2}-(\frac{blnb-alna}{b-a}-1)$=$\frac{1}{b-a}[{(b-a)ln\frac{a+b}{2}-blnb+alna+b-a}]$.
设函数$g(x)=(x-a)ln\frac{x+a}{2}-xlnx+alna+x-a$,x∈(0,+∞),
则$g'(x)=ln\frac{x+a}{2x}+\frac{x-a}{x+a}$,$g''(x)=\frac{a(x-a)}{{x{{(x+a)}^2}}}$.
当x>a时,g''(x)>0,所以g'(x)在(a,+∞)上单调递增;
又g'(x)>g'(a)=0,因此g(x)在(a,+∞)上单调递增.
又b>a,所以g(b)>g(a)=0,即A-C>0,即A>C.
(iii)$C-B=\frac{blnb-alna}{b-a}-1-\frac{lna+lnb}{2}$=$\frac{1}{b-a}(\frac{a+b}{2}lnb-\frac{a+b}{2}lna+a-b)$.
设$h(x)=\frac{x+a}{2}lnx-\frac{x+a}{2}lna-x+a$,x∈(0,+∞).
则$h'(x)=\frac{1}{2}lnx+\frac{a}{2x}-\frac{1}{2}lna-\frac{1}{2}$,有$h''(x)=\frac{x-a}{{2{x^2}}}$.
当x>a时,h''(x)>0,所以h'(x)在(a,+∞)上单调递增,有h'(x)>h'(a)=0.
所以h(x)在(a,+∞)上单调递增.
又b>a,所以h(b)>h(a)=0,即C-B>0,故C>B.
综上可知:A>C>B.
点评 本题主要考查了函数的构造和利用导函数判断函数的单调性,难点是对题意的转化和函数的构造.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
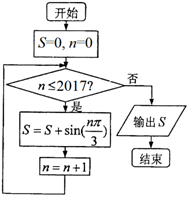
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 “杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )
“杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,如图是三角形数阵,记an为图中第n行各个数之和,则a5+a11的值为( )| A. | 528 | B. | 1020 | C. | 1038 | D. | 1040 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
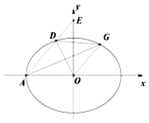 如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.
如图,在平面直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A(-2,0),离心率为$\frac{\sqrt{2}}{2}$,过A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴为E,过点O作直线l的平行线交椭圆于点G,设△AOD,△AOE,△DOG的面积分别为S1、S2、S3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com