
分析 由集合A,B,C间的包含关系进行求解,即可求得答案,其中应注意运用分类讨论的数学思想.
解答 解:A={x|x2-3x+2=0}={1,2},B={x∈R|x2-ax+a-1=0},C={x∈R|x2-bx+2=0},
∵x=1是方程x2-ax+a-1=0的解,
∴B≠∅,
而B?A,∴B={1},可以解得a=2,
由C⊆A,进行分类讨论:
①若C=∅,则△<0,∴$-2\sqrt{2}$<b<2$\sqrt{2}$;
②若C={1}或{2}时,△=0,∴b=$±2\sqrt{2}$,此时,C={$\sqrt{2}$}或{-$\sqrt{2}$},不合题意,故舍去;
③若C={1,2}时,解得b=3,
综上,实数a,b的取值分别为a=2,b=3或-2$\sqrt{2}$<b<2$\sqrt{2}$.
点评 本题考查集合间的包含关系的应用,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1-i | B. | 1+i | C. | $\frac{1}{2}+\frac{1}{2}i$ | D. | $\frac{1}{2}-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在平行四边形OABC中,点E,F分别在AB,BC上,且满足AB=2AE,BC=3CF.若$\overrightarrow{OB}$=λ$\overrightarrow{OE}$+μ$\overrightarrow{OF}$(λ、μ∈R),则λ+μ=$\frac{7}{5}$.
如图,在平行四边形OABC中,点E,F分别在AB,BC上,且满足AB=2AE,BC=3CF.若$\overrightarrow{OB}$=λ$\overrightarrow{OE}$+μ$\overrightarrow{OF}$(λ、μ∈R),则λ+μ=$\frac{7}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错 | B. | 小前提错 | ||
| C. | 推理形式错 | D. | 大前提和小前提都错 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
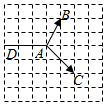
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{5}{2}$ | D. | $-\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com