
| 17π |
| 4 |
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
 “菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,如果烟花距地面高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?
“菊花”烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂,如果烟花距地面高度h m与时间t s之间的关系为h(t)=-4.9t2+14.7t+18,那么烟花冲出后什么时候是它爆裂的最佳时刻?这时距地面的高度是多少(精确到1m)?查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 男 | 女 | 总计 | |
| 达标 | a=24 | b= | |
| 不达标 | c= | d=12 | |
| 总计 | n=50 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
| n(ad-bc)2 |
| (a+c)(b+d)(a+b)(c+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
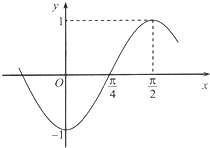 已知函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)部分图象如图所示.
已知函数f(x)=Asin(ωx+φ),(ω>0,|φ|<π)部分图象如图所示.| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 身高达标 | 身高不达标 | 总计 | |
| 积极参加体育锻炼 | 40 | 35 | 75 |
| 不积极参加体育锻炼 | 10 | 15 | 25 |
| 总计 | 50 | 50 | 100 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com