练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．a，b，c，d四位同学各自对甲、乙两变量做回归分析，分别得到散点图与残差平方和$\sum_{i=1}^{n}$（yi-$\widehat{{y}_{i}}$）2如下表：
    abcd
    散点图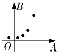
    残差平方和115106124103
    哪位同学的实验结果体现拟合甲、乙两变量关系的模型拟合精度高？（　　）
    A．aB．bC．cD．d

    分析 根据散点图以及残差平方和的大小进行判断即可．

    解答 解：由散点图可知D的残差平方和最小，此时图象和回归方程拟合精度高，
    故选：D

    点评 本题主要考查散点图和残差平方和的应用，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．如图，F是抛物线E：y2=2px（p＞0）的焦点，A是抛物线E上任意一点．现给出下列四个结论：
    ①以线段AF为直径的圆必与y轴相切；②当点A为坐标原点时，|AF|为最短；
    ③若点B是抛物线E上异于点A的一点，则当直线AB（AB≥2P）过焦点F时，|AF|+|BF|取得最小值；
    ④点B、C是抛物线E上异于点A的不同两点，若|AF|、|BF|、|CF|成等差数列，则点A、B、C的横坐标亦成等差数列．其中正确结论的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知f（x）=$\left\{\begin{array}{l}{x+2（x≤-1）}\\{{x}^{2}（x＞-1）}\end{array}\right.$，若f（x）=3，则x的值是（　　）
    A．1B．1或±$\sqrt{3}$C．±$\sqrt{3}$D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．直线y=kx+b通过第一、三、四象限，则有（　　）
    A．d＞0，b＞0B．k＞0，b＜0C．k＜0，b＞0D．k＜0，b＜0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知圆C的方程为x2-y2-2x-4y+m=0
    （1）若圆C的半径为2，求m的值
    （2）若圆C与直线l：x+2y-4=0相交于M，N两点，且|MN|=$\frac{4\sqrt{5}}{5}$，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某医院眼科某天测量300名求医者的视力情况，得到频率分布直方图如图所示，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列．
    （1）求出最大频率；
    （2）求出视力在4.6-5.0的人数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知sinx+cosx=$\sqrt{1+sin2x}$，则x的取值范围是（　　）
    A．[-$\frac{π}{4}$+kπ，$\frac{π}{4}$+kπ]（k∈Z）B．[$\frac{π}{4}$+kπ，$\frac{3π}{4}$+kπ]（k∈Z）
    C．[-$\frac{π}{4}$+2kπ，$\frac{3π}{4}$+2kπ]（k∈Z）D．[$\frac{π}{4}$+2kπ，$\frac{5π}{4}$+2kπ]（k∈Z）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．设复数z=1-i，若实数a，b满足z2+az+b=$\overline{z}$，则|a+bi|=5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=3x，f（a+2）=81，g（x）=$\frac{1-{a}^{x}}{1+{a}^{x}}$．
    （1）求g（x）的解析式并判别g（x）的奇偶性；
    （2）用定义证明：函数g（x）在R上是单调递减函数；
    （3）求函数g（x）的值域．

    查看答案和解析>>

    同步练习册答案