Question

圆O₁和圆O₂的极坐标方程分别为ρ＝4cosθ，ρ＝－4sinθ.

(1) 把圆O₁和圆O₂的极坐标方程化为直角坐标方程；

(2) 求经过圆O₁、圆O₂交点的直线的直角坐标方程．

Answer 1

解：以极点为原点、极轴为x轴正半轴建立平面直角坐标系，两坐标系中取相同的长度单位．

(1) x＝ρcosθ，y＝ρsinθ，由ρ＝4cosθ得ρ²＝4ρcosθ，所以x²＋y²＝4x.即圆O₁的直角坐标方程为x²＋y²－4x＝0，同理圆O₂的直角坐标方程为x²＋y²＋4y＝0.

(2) 由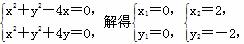即圆O₁、圆O₂交于点(0，0)和(2，－2)，故过交点的直线的直角坐标方程为y＝－x.

由于平面上点的极坐标的表示形式不唯一，即(ρ，θ)，(ρ，2π＋θ)，(－ρ，π＋θ)，(－ρ，－π＋θ)，都表示同一点的坐标，这与点的直角坐标的唯一性明显不同．所以对于曲线上的点的极坐标的多种表示形式，只要求至少有一个能满足极坐标方程即可．例如对于极坐标方程ρ＝θ，点M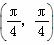可以表示为等多种形式，其中，只有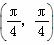的极坐标满足方程ρ＝θ.