练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在△ABC中，已知CM是∠ACB的平分线，△AMC的外接圆交BC于点N.若AC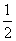＝AB，求证：BN＝2AM.


    证明： 在△ABC中，因为CM是∠ACB的角平分线，所以＝.

    又已知AC＝AB，所以＝.①

    又BA与BC是圆O过同一点B的割线，

    所以BM·BA＝BN·BC，即＝.②

    由①②可知，＝，所以BN＝2AM.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知矩阵A＝，若点P(1，1)在矩阵A对应的变换作用下得到点P′(0，－8)．

    (1) 求实数a的值；

    (2) 求矩阵A的特征值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    圆O1和圆O2的极坐标方程分别为ρ＝4cosθ，ρ＝－4sinθ.

    (1) 把圆O1和圆O2的极坐标方程化为直角坐标方程；

    (2) 求经过圆O1、圆O2交点的直线的直角坐标方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


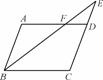
    如图，在ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE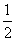＝CD.

    (1) 求证：△ABF∽△CEB；

    (2) 若△DEF的面积为2，求ABCD的面积．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，已知P是圆O外一点，PD为圆O的切线，D为切点，割线PEF经过圆心O，若PF＝12，PD＝4 ，求圆O的半径长和∠EFD的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在△ABC中，∠C＝90°，∠A＝60°，AB＝20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，求DE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    解不等式：|x＋1|>3.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|x＋a|＋|x－2|.

    (1) 当a＝－3时，求不等式f(x)≥3的解集；

    (2) 若f(x)≤|x－4|的解集包含[1，2]，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ax2＋bx＋c，且f(1)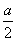＝－，3a＞2c＞2b，求证：

    (1)a＞0，且－3＜＜－；

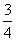    (2)函数f(x)在区间(0,2)内至少有一个零点；

    (3)设x1，x2是函数f(x)的两个零点，则≤|x1－x2|＜.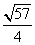

    查看答案和解析>>

    同步练习册答案