设函数f(x)＝ax2＋bx＋c，且f(1)＝－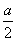
，3a＞2c＞2b，求证：
(1)a＞0，且－3＜
＜－
；
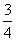(2)函数f(x)在区间(0,2)内至少有一个零点；
(3)设x1，x2是函数f(x)的两个零点，则
≤|x1－x2|＜
.
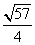解析： (1)由已知得f(1)＝a＋b＋c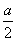＝－，∴3a＋2b＋2c＝0，
又3a>2c>2b，∴a＞0，b＜0.
又2c＝－3a－2b，∴3a＞－3a－2b＞2b，
∵a＞0，∴－3＜＜－.
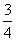(2)由已知得f(0)＝c，f(2)＝4a＋2b＋c＝a－c，
①当c＞0时，f(0)＝c＞0，f(1)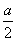＝－＜0，
∴函数f(x)在区间(0,1)内至少有一个零点；
②当c≤0时，f(1)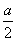＝－＜0，f(2)＝a－c＞0，
∴函数f(x)在区间(1,2)内至少有一个零点．
综上所述，函数f(x)在区间(0,2)内至少有一个零点．
(3)∵x1，x2是函数f(x)的两个零点，
∴x1＋x2＝－，x1x2＝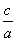
＝－
－，
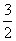∴|x1－x2|＝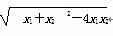
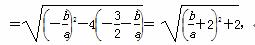
∵－3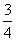＜＜－，∴≤|x1－x2|＜.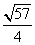
科目：高中数学 来源： 题型：
已知f(x)＝32x－(k＋1)3x＋2，当x∈R时，f(x)恒为正值，则k的取值范围是( )
A．(－∞，－1) B．(－∞，2－1)
C．(－1,2－1) D．(－2－1,2－1)
查看答案和解析>>
科目：高中数学 来源： 题型：
已知集合A、B，定义集合A与B的一种运算A⊕B，其结果如下表所示：
| A | {1,2,3,4} | {－1,1} | {－4,8} | {－1,0,1} |
| B | {2,3,6} | {－1,1} | {－4，－2,0,2} | {－2，－1,0,1} |
| A⊕B | {1,4,6} | ∅ | {－2,0,2,8} | {－2} |
按照上述定义，若M＝{－2 011,0,2 012}，N＝{－2 012,0,2 013}，则M⊕N＝________.
查看答案和解析>>
科目：高中数学 来源： 题型：
若数列{an}满足：存在正整数T，对于任意正整数n都有an＋T＝an成立，则称数列{an}为周期数列，周期为T.已知数列{an}满足a1＝m(m＞0)，an＋1＝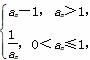
则下列结论中错误的是( )
A．若m＝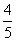
，则a5＝3 B．若a3＝2，则m可以取3个不同的值
C．若m＝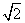
，则数列{an}是周期为3的数列 D．∃m∈Q且m≥2，使得数列{an}是周期数列
查看答案和解析>>
科目：高中数学 来源： 题型：
下列函数中，为偶函数且有最小值的是( )
A．f(x)＝x2＋x B．f(x)＝|ln x|
C．f(x)＝xsin x D．f(x)＝ex＋e－x
查看答案和解析>>
科目：高中数学 来源： 题型：
设f(n)是定义在N*上的增函数，f(4)＝5，且满足：
①任意n∈N*，f(n)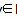 
Z；②任意m，n∈N*，有f(m)f(n)＝f(mn)＋f(m＋n－1)．
（1）求f(1)，f(2)，f(3)的值；（2）求f(n)的表达式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
AB，求证：BN＝2AM.
D.