
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 根据回归直线方程过样本点中心判断(1)正确;
用数学归纳法证明时第一步令n=1求出等式左边式子即可判断(2)正确;
x+$\frac{1}{x}$≥2在x>0恒成立,x<0不成立,判断(3)错误;
判断“am2<bm2”是“a<b”的充分不必要条件,得(4)错误.
解答 解:对于(1),根据回归直线方程$\hat y=\hat bx+\hat a$必过样本点中心($\overline{x}$,$\overline{y}$),判断(1)正确;
对于(2),数学归纳法证明等式1+2+3+…+2n=$\frac{{2}^{n}({2}^{n}+1)}{2}$(n≥2,n∈N*)时,
第一步是n=1,等式左边为1+2,命题(2)正确;
对于(3),关于实数x的不等式关系x+$\frac{1}{x}$≥2在x>0恒成立,
x<0不成立,∴命题(3)错误;
对于(4),“am2<bm2”时,“a<b”成立,充分性成立;
“a<b”时,“am2<bm2”不成立,必要性不成立;
是充分不必要条件,(4)错误.
综上,正确的命题序号是(1)、(2)共2个.
故选:C.
点评 本题考查了线性回归方程、数学归纳法以及基本不等式的应用问题,也考查了命题真假的应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{10}$ | B. | $\frac{3π}{20}$ | C. | $1-\frac{3π}{10}$ | D. | $1-\frac{3π}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 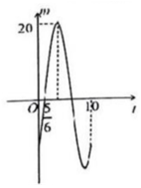 | B. |  | C. |  | D. | 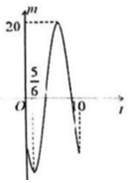 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-3,2)\;\;\;\;\;\;\;\sqrt{13}$ | B. | $(3,-2)\;\;\;\;\;\;\;\sqrt{13}$ | C. | (-3,2)4 | D. | (3,-2)4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4,5} | B. | {1,4} | C. | {1,2,4} | D. | {3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
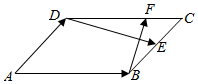 如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;
如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $A_{26-m}^7$ | B. | $C_{26-m}^7$ | C. | $A_{20-m}^7$ | D. | $A_{26-m}^6$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com