
分析 (I)由(a+b)(sinA-sinB)=(c-b)sinC,由正弦定理可得:(a+b)(a-b)=(c-b)c,化为b2+c2-a2=bc.再利用余弦定理可得:cosA.
(II)f(x)=$\frac{\sqrt{3}}{2}$sinx+$\frac{1+cosx}{2}$=$sin(x+\frac{π}{6})$+$\frac{1}{2}$,在锐角△ABC中,$\frac{π}{6}$<B$<\frac{π}{2}$,可得$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,即可得出.
解答 解:(I)∵(a+b)(sinA-sinB)=(c-b)sinC,由正弦定理可得:(a+b)(a-b)=(c-b)c,化为b2+c2-a2=bc.
由余弦定理可得:cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{bc}{2bc}$=$\frac{1}{2}$,
∵A∈(0,π),∴A=$\frac{π}{3}$.
(II)f(x)=$\sqrt{3}sin\frac{x}{2}•cos\frac{x}{2}+{cos^2}\frac{x}{2}$=$\frac{\sqrt{3}}{2}$sinx+$\frac{1+cosx}{2}$=$sin(x+\frac{π}{6})$+$\frac{1}{2}$,
在锐角△ABC中,$\frac{π}{6}$<B$<\frac{π}{2}$,∴$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,
∴$sin(B+\frac{π}{6})$∈$(\frac{\sqrt{3}}{2},1]$,
∴f(B)的取值范围是$(\frac{1+\sqrt{3}}{2},\frac{3}{2}]$.
点评 本题考查了正弦定理余弦定理、和差公式、三角函数的单调性,考查了推理能力 与计算能力,属于中档题.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{f(x)}$ | B. | y=lg[1-f(x)] | C. | y=${\frac{1}{2}}^{f(x)}$ | D. | y=|f(x)| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\sqrt{3}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4} | B. | {0,2,4} | C. | {2,4} | D. | {3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
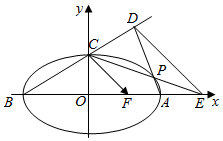 如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.
如图:A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的顶点,点F(c,0)为椭圆的右焦点,原点O到直线CF的距离为$\frac{1}{2}c$,且椭圆过点$({2\sqrt{3},1})$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 输出使1×2×4×…×n≥2015成立的最小整数n | |
| B. | 输出使1×2×4×…×n≥2015成立的最大整数n | |
| C. | 输出使1×2×4×…×n≥2015成立的最大整数n+2 | |
| D. | 输出使1×2×4×…×n≥2015成立的最小整数n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com