
| π |
| 6 |
| π |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
| 2bx+3sinx+bxcosx |
| 2+cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 25 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
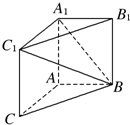 如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.查看答案和解析>>
科目:高中数学 来源: 题型:
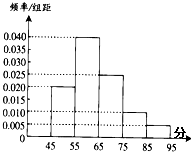 为了调查某班学生做数学题的基本能力,随机抽查了部分学生某次做一份满分为100分的数学试题,他们所得分数的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图,则这些学生的平均分为
为了调查某班学生做数学题的基本能力,随机抽查了部分学生某次做一份满分为100分的数学试题,他们所得分数的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图,则这些学生的平均分为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com