
分析 利用和角的正弦公式,结合点($\frac{π}{6}$,$\frac{1}{2}$)在函数y=f(2x+$\frac{π}{6}$)的图象上,求出φ的值.
解答 解:因为f(x)=sinxcosφ+cosxsinφ=sin(x+φ),
所以y=f(2x+$\frac{π}{6}$)=sin(2x+$\frac{π}{6}$+φ),
∵点($\frac{π}{6}$,$\frac{1}{2}$)在函数y=f(2x+$\frac{π}{6}$)的图象上,
∴sin(2×$\frac{π}{6}$+$\frac{π}{6}$+φ)=$\frac{1}{2}$,
∴cosφ=$\frac{1}{2}$,
∵0<φ<π,∴φ=$\frac{π}{3}$.
故答案为$\frac{π}{3}$.
点评 本题考查和角的正弦公式,考查三角函数的图象与性质,比较基础.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{1}{8}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x) | B. | -f(x) | C. | g(x) | D. | -g(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (-2,0) | C. | (0,2) | D. | (0,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
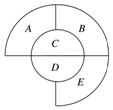 已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有18种.
已知一个公园的形状如图所示,现有3种不同的植物要种在此公园的A,B,C,D,E这五个区域内,要求有公共边界的两块相邻区域种不同的植物,则不同的种法共有18种.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com