Question

4．观察下列等式：

照以上式子规律：
（1）写出第5个等式，并猜想第n个等式； （n∈N^*）
（2）用数学归纳法证明上述所猜想的第n个等式成立．（n∈N^*）

Answer 1

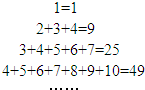
分析 （1）通过前4个表达式，直接写出第5个等式，并猜想第n个等式；（n∈N^*）
（2）用数学归纳法证明步骤，直接证明上述所猜想的第n个等式成立．（n∈N^*）

解答 解：（1）第5个等式为：5+6+7+8+9+10+11+12+13=9²…（2分）
第n个等式为：n+（n+1）+（n+2）+…+（3n-2）=（2n-1）²，n∈N^*…（5分）
（2）①当n=1时，等式左边=1，等式右边=（2-1）²=1，所以等式成立．…（6分）
②假设n=k（k∈N^*）时，等式成立，即k+（k+1）+（k+2）+…+（3k-2）=（2k-1）²（k≥1，k∈N^*）
那么，当n=k+1时，（k+1）+（k+2）+（k+3）+…+（3k+1）=k+（k+1）+（k+2）+…+（3k-2）+（3k-1）+3k+（3k+1）-k=（2k-1）²+8k=[2（k+1）-1）²，
即n=k+1时等式成立．…（11分）
根据（1）和（2），可知对任何n∈N^*，等式都成立．…（12分）

点评 本题考查数学归纳法证明猜想成立，注意证明步骤的应用，缺一不可．