
| A�� | ������10����ʱ������һ����145.83cm | |
| B�� | ������10����ʱ��������145.83cm���� | |
| C�� | ������10����ʱ��������145.83cm���� | |
| D�� | ������10����ʱ��������145.83cm���� |
���� ���������ĸ�������Ļع�ģ�ͣ����Թ��ƺ�����10��ʱ���ܵ����ߣ�����һ��Ԥ��ֵ������ȷ����ֵ��������ʱע�ⲻҪ������
��� �⣺������������Ļع�ģ��Ϊ$\widehat{y}$=7.19x+73.93��
�����Ԥ������10��ʱ��������$\widehat{y}$=7.19x+73.93=7.19��10+73.93=145.83��
��������10��ʱ��������145.83cm���ң�
��ѡ��C��
���� ���⿼��ع�����ij���Ӧ�ã���һ�������⣬���ָ��ݻع�ֱ�߷���Ԥ�����Ľ������һ������ֵ������ȷ����ֵ��������ĿҪ�����֪ʶ�㣮


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
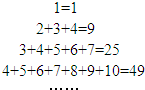
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 657 | B�� | 757 | C�� | 688 | D�� | 788 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ | B�� | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | C�� | $\frac{{\sqrt{2}+\sqrt{6}}}{4}$ | D�� | -$\frac{{\sqrt{2}+\sqrt{6}}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | 10 | C�� | 11 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-7��+�ޣ� | B�� | ��-7��$\frac{1}{2}}$���ȣ�${\frac{1}{2}$��+�ޣ� | C�� | [-7��+�ޣ� | D�� | [-7��$\frac{1}{2}}$���ȣ�${\frac{1}{2}$��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com