
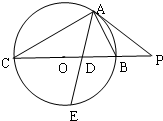
 如图,△ABC内接于直径为F1,F2的圆P,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10
如图,△ABC内接于直径为F1,F2的圆P,过点A作圆O的切线交CB的延长线于点P,∠BAC的平分线分别交BC和圆O于点D、E,若PA=2PB=10| AC |
| AB |
| AP |
| PB |
| AC |
| AB |
| CD |
| DB |


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| A、f(1)>ef(0)>e2f(-1) |
| B、f(1)<ef(0)<e2f(-1) |
| C、e2f(-1)>ef(0)>f(1) |
| D、e2f(-1)<ef(0)<f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| P0B |
| 1 |
| 4 |
| AB |
| PB |
| PC |
| P0B |
| P0C |
| π |
| 3 |
| AC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 第一首歌专业评审团全票通过概率 | 第二首歌三分之二以上专业评审团通过概率 | 第三首歌三分之二以上媒体评审团通过概率 | 第三首歌媒体评审团全票通过概率 |
| 0.2 | 0.5 | 0.8 | 0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com