
分析 (Ⅰ)当a=1时,不等式|f(x)|+|f(-x)|≥3x即|x-1|+|x+1|≥3x,分类讨论,即可解不等式|f(x)|+|f(-x)|≥3x;
(Ⅱ)设|a|≤1,当|x|≤1时,|f(x2)+x|≤|a|(1-x2)+|x|≤1-x2+|x|,即可证明:$|f({x^2})+x|≤\frac{5}{4}$.
解答 解:( I)当a=1时,不等式|f(x)|+|f(-x)|≥3x即|x-1|+|x+1|≥3x
当x≤-1时,得1-x-x-1≥3x⇒x≤0,∴x≤-1-----------------------------------------(1分)
当-1<x<1时,得1-x+x+1≥3x$⇒x≤\frac{2}{3}$,∴$-1<x≤\frac{2}{3}$-----------------------------(2分)
当x≥1时,得x-1+x+1≥3x⇒x≤0,与x≥1矛盾,-------------------------------------(3分)
综上得原不等式的解集为$\{x|x≤-1\}∪\{x|-1<x≤\frac{2}{3}\}$=$\{x|x≤\frac{2}{3}\}$------------------------(5分)
(II)证明:|f(x2)+x|=|a(x2-1)+x|≤|a(x2-1)|+|x|-----------------------------------------------(6分)
∵|a|≤1,|x|≤1
∴|f(x2)+x|≤|a|(1-x2)+|x|≤1-x2+|x|-------------------------------------------------(7分)
=$-|x{|^2}+|x|+1=-{(|x|-\frac{1}{2})^2}+\frac{5}{4}≤\frac{5}{4}$,------------------------------------------(9分)
当$|x|=\frac{1}{2}$时取“=”,得证.--------------------------------------------------------------(10分)
点评 本题考查不等式的解法,考查绝对值不等式的性质,正确转化是关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2(e-1)}$ | B. | $\frac{1}{4(e-1)}$ | C. | $\frac{1}{8(e-1)}$ | D. | $\frac{1}{16(e-1)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 选择自然科学类 | 选择社会科学类 | 合计 | |
| 男生 | 60 | 45 | 105 |
| 女生 | 30 | 45 | 75 |
| 合计 | 90 | 90 | 180 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
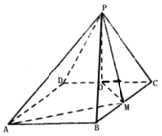 如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )
如图,四边形ABCD为矩形,平面PCD⊥平面ABCD,且PC=PD=CD=2,BC=2$\sqrt{2}$,O,M分别为CD,BC的中点,则异面直线OM与PD所成角的余弦值为( )| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{3}}{6}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com