
���� �٣�������x2+2x+m=0��ʵ�������=22-4m��0⇒m��1⇒m��2��
�ڣ���˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$��һ��������б��Ϊ2����$\frac{b}{a}=2$����������Ϊ$\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}=\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}=\sqrt{5}$��
�ۣ�����ǡ�ABC�У�A+B$��\frac{��}{2}$⇒$\frac{��}{2}$A��$\frac{��}{2}-B$��0⇒sinA��cosB������
�ܣ��ؾ����㷨���ص����ڰ���һ��n�ζ���ʽ��ֵת��Ϊ��n��һ�ζ���ʽ��ֵ��
�ݣ����ģ�ⷽ���ĵ�����Ƿ�•ŵ�������ʴ���
��� �⣺���ڢ٣�������x2+2x+m=0��ʵ�������=22-4m��0⇒m��1⇒m��2������ȷ��
���ڢڣ���˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1��{a��0��b��0}��$��һ��������б��Ϊ2����$\frac{b}{a}=2$����������Ϊ$\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}=\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}=\sqrt{5}$������ȷ��
���ڢۣ�����ǡ�ABC�У�A+B$��\frac{��}{2}$⇒$\frac{��}{2}$A��$\frac{��}{2}-B$��0⇒sinA��cosB����������ȷ��
���ڢܣ��ؾ����㷨���ص����ڰ���һ��n�ζ���ʽ��ֵת��Ϊ��n��һ�ζ���ʽ��ֵ����ȷ��
���ڢݣ����ģ�ⷽ���ĵ�����Ƿ�•ŵ�������ʴ���
�ʴ�Ϊ���٢ڢۢ�
���� ���⿼����������ٵ��ж������ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
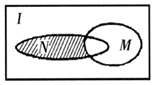 ��ȫ��I��ʵ����R��M={x|x��3}��N={x|��x-3����x-1����0}����I���Ӽ�����ͼ��ʾ��������Ӱ��������ʾ�ļ���Ϊ��������
��ȫ��I��ʵ����R��M={x|x��3}��N={x|��x-3����x-1����0}����I���Ӽ�����ͼ��ʾ��������Ӱ��������ʾ�ļ���Ϊ��������| A�� | {x|1��x��3} | B�� | {x|1��x��3} | C�� | {x|1��x��3} | D�� | {x|1��x��3} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{7}$ | B�� | $\frac{3}{7}$ | C�� | $\frac{4}{7}$ | D�� | $\frac{5}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com