
分析 先利用同角三角函数的基本关系求得2θ的范围以及sin2θ的值,可得2θ的值,从而求得cos2θ的值,再利用两角差的余弦公式求得cos(2θ+$\frac{π}{3}}$)的值.
解答 解:∵$θ∈({\frac{π}{2},π}),\frac{1}{sinθ}+\frac{1}{cosθ}=2\sqrt{2}$,∴sinθ>0,cosθ<0,
∴$\frac{sinθ+cosθ}{sinθ•cosθ}$=2$\sqrt{2}$,即sinθ+cosθ=2$\sqrt{2}$sinθcosθ<0,∴θ∈($\frac{3π}{4}$,π),2θ∈($\frac{3π}{2}$,2π).
再根据sinθ+cosθ=-$\sqrt{{(sinθ+cosθ)}^{2}}$=-$\sqrt{1+2sinθcosθ}$,
∴2$\sqrt{2}$sinθcosθ=-$\sqrt{1+2sinθcosθ}$,∴sinθcosθ=$\frac{1}{2}$ (舍去),或sinθcosθ=-$\frac{1}{4}$,
即sin2θ=-$\frac{1}{2}$,∴2θ=$\frac{11π}{6}$,∴cos2θ=$\sqrt{{1-sin}^{2}2θ}$=$\frac{\sqrt{3}}{2}$.
则$cos({2θ+\frac{π}{3}})$=cos2θcos$\frac{π}{3}$-sin2θsin$\frac{π}{3}$=$\frac{\sqrt{3}}{4}$-(-$\frac{\sqrt{3}}{4}$)=$\frac{\sqrt{3}}{2}$,
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题主要考查同角三角函数的基本关系,两角差的余弦公式的应用,属于基础题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:解答题
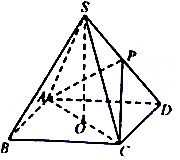 如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.
如图,在四棱锥S-ABCD中,点O是正方形ABCD的中心,SO⊥平面ABCD,且SO=OD,点P为棱SD上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
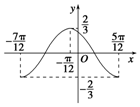
| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m=20,n=10 | B. | m=10,n=20 | C. | m=21,n=10 | D. | m=11,n=21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2) | B. | (-∞,-1]∪[2,+∞) | C. | [-1,2] | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{2}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com