
| A. | y=$\frac{2}{3}$sin(2x+$\frac{π}{3}$) | B. | y=$\frac{2}{3}$sin($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=$\frac{2}{3}$sin(x-$\frac{π}{3}$) | D. | y=$\frac{2}{3}$sin(2x+$\frac{2}{3}$π) |
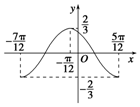
分析 根据图象的最高点和最低点求出A,根据周期T=$\frac{5π}{12}-(-\frac{7π}{12})$求ω,图象过($-\frac{π}{12},\frac{2}{3}$),代入求φ,即可求函数f(x)的解析式;
解答 解:由图象的最高点$\frac{2}{3}$,最低点-$\frac{2}{3}$可得A=$\frac{2}{3}$,
周期T=$\frac{5π}{12}-(-\frac{7π}{12})$=π,
∴$ω=\frac{2π}{T}=2$.
图象过($-\frac{π}{12},\frac{2}{3}$),
∴$\frac{2}{3}=\frac{2}{3}Sin(2×-\frac{π}{12}+φ)$,
可得:φ=$2kπ+\frac{2π}{3}$.
则解析式为y=$\frac{2}{3}$sin(2x+$\frac{2π}{3}+2kπ$)=$\frac{2}{3}sin(2x+\frac{2π}{3})$
故选:D.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系.


科目:高中数学 来源: 题型:解答题
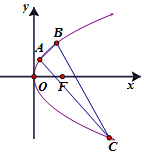 给定直线l:y=2x-16,抛物线G:y2=ax(a>0)
给定直线l:y=2x-16,抛物线G:y2=ax(a>0)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
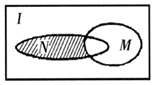 设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )
设全集I是实数集R,M={x|x≥3}与N={x|(x-3)(x-1)≤0}都是I的子集(如图所示),则阴影部分所表示的集合为( )| A. | {x|1<x<3} | B. | {x|1≤x<3} | C. | {x|1<x≤3} | D. | {x|1≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{5π}{6},\frac{π}{12}}]$ | B. | $[{-\frac{π}{3},\frac{π}{6}}]$ | C. | $[{-\frac{π}{6},\frac{π}{3}}]$ | D. | $[{\frac{π}{6},\frac{2π}{3}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com