
分析 (1)由三角函数的公式化简可得f(x)═$\frac{1}{2}$sin(2x-$\frac{π}{6}$)+$\frac{1}{4}$,由周期公式可得周期,和最大值,
(2)f(C)=$\frac{3}{4}$,代入求得C=$\frac{π}{3}$,由三角形的面积公式S=$\frac{1}{2}$absinC,求得b,根据余弦定理求得c的值.
解答 解:(1)f(x)=sinx•cos(x-$\frac{π}{6}$)=sinx(cosxcos$\frac{π}{6}$+sinxsin$\frac{π}{6}$)
=$\frac{\sqrt{3}}{2}$sinxcosx-$\frac{1}{4}$(-2sin2x+1)+$\frac{1}{4}$,
=$\frac{\sqrt{3}}{4}$sin2x-$\frac{1}{4}$cos2x+$\frac{1}{4}$,
=$\frac{1}{2}$sin(2x-$\frac{π}{6}$)+$\frac{1}{4}$,
∴求f(x)的最小正周期T=$\frac{2π}{ω}$=π,
最大值:$\frac{3}{4}$,
(2)若f(C)=$\frac{3}{4}$,b=4,
∴f(C)=$\frac{1}{2}$sin(2C-$\frac{π}{6}$)+$\frac{1}{4}$=$\frac{3}{4}$,
∴sin(2C-$\frac{π}{6}$)=1,
∴2C-$\frac{π}{6}$=$\frac{π}{2}$,C=$\frac{π}{3}$,
S=$\frac{1}{2}$absinC,
∴a=2,
由余弦定理c2=a2+b2-2abcosC,
∴c=2$\sqrt{3}$.
点评 本题考查三角恒等变换、求正弦函数周期和最值及余弦定理,属于中档题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{191}{32}$ | B. | -$\frac{191}{32}$ | C. | $\frac{95}{16}$ | D. | -$\frac{95}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 等腰三角形 | C. | 直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
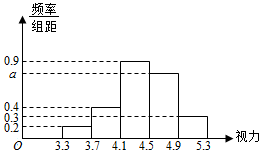 某市教育主管部门为调查该市高三学生的视力情况,从全市随机抽取了100名学生迸行检测,并将视力以[3.3,3.7),[3.7,4.1),[4.1,4.5),[4.5,4.9),[4.9,5.3]分段进行统计,得到如图所示的频率分布直方图.
某市教育主管部门为调查该市高三学生的视力情况,从全市随机抽取了100名学生迸行检测,并将视力以[3.3,3.7),[3.7,4.1),[4.1,4.5),[4.5,4.9),[4.9,5.3]分段进行统计,得到如图所示的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com