
设函数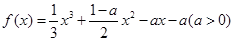 .
.
(1)若函数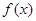 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数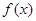 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
(1)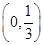 (2)
(2)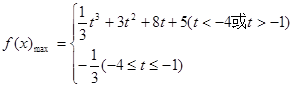
解析试题分析:
科目:高中数学
来源:
题型:解答题
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
(1)根据题意对函数 求导,获得导函数
求导,获得导函数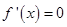 的根与大于0小于0的解集,获得函数
的根与大于0小于0的解集,获得函数 的单调区间和极值点,极值.进而确定函数
的单调区间和极值点,极值.进而确定函数 在区间
在区间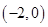 上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在
上的单调性,再利用数形结合的思想与零点存在性定理的知识可以得到函数在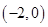 上要有两个零点,需要
上要有两个零点,需要 满足
满足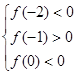 即可,解不等式即可求出
即可,解不等式即可求出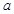 的取值范围.
的取值范围.
(2)根据题意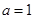 ,则利用(1)可以得到
,则利用(1)可以得到 的单调性以及极值点,极值.要得到函数
的单调性以及极值点,极值.要得到函数 在含参数的区间
在含参数的区间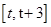 上的最大值,我们需要讨论
上的最大值,我们需要讨论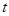 的范围得到函数
的范围得到函数 的在区间
的在区间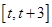 上的单调性进而得到
上的单调性进而得到 在该区间上的最大值,为此分三种情况分别为
在该区间上的最大值,为此分三种情况分别为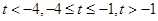 ,依次确定单调性得到最大值即可.
,依次确定单调性得到最大值即可.
试题解析:
(1)∵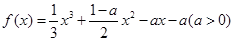
∴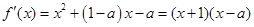 , (1分)
, (1分)
令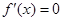 ,解得
,解得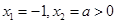 (2分)
(2分)
当x变化时,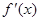 ,
,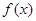 的变化情况如下表:
的变化情况如下表:
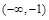
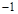


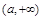
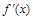
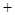
0 — 0 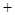
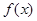
↗ 极大值 ↘ 极小值 

千里马英语完形填空与阅读理解系列答案
奇速英语系列答案
牛津英语学习全攻略同步阅读系列答案
魔法教程字词句段篇章系列答案
智慧阅读系列答案
中华活页文选系列答案
中考达标学案系列答案
黑皮系列分层强化训练系列答案
全品新阅读系列答案
150加50篇英语完形填空与阅读理解系列答案
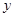 (升)与行驶速度
(升)与行驶速度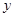 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(1)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号