练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知集合U=R，集合A={x|x≥1}，B={x|0＜x＜4}，则（∁UA）∩B=（　　）
    A．{x|x＜1或x≥4}B．{x|0＜x＜1}C．{x|1≤x＜4}D．{x|x＜4}

    分析 根据补集与交集的定义，进行运算即可．

    解答 解：∵集合U=R，集合A={x|x≥1}，B={x|0＜x＜4}，
    ∴∁UA={x|x＜1}
    ∴（∁UA）∩B={x|0＜x＜1}．
    故选：B．

    点评 本题考查了集合的定义与运算问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．已知向量$\overrightarrow{a}$=（2，3），向量$\overrightarrow{b}$=（x，-2），且$\overrightarrow{a}$与2$\overrightarrow{a}$-$\overrightarrow{b}$共线，则实数x的值为-$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若复数z满足z（2-i）=10+5i（i为虚数单位），则|z|=（　　）
    A．25B．10C．5D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

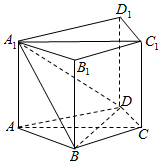    10．如图，在直四棱柱ABCD-A1B1C1D1中，∠BAD=60°，AB=BD，BC=CD．
    （1）求证：平面ACC1A1⊥平面A1BD；
    （2）当BC⊥CD时，直线BC与平面A1BD所成的角能否为45°？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设集合A={x|4x2≤1}，B={x|lnx＜0}，则A∩B=（　　）
    A．$（-\frac{1}{2}，\frac{1}{2}）$B．$（0，\frac{1}{2}）$C．$[\frac{1}{2}，1）$D．$（0，\frac{1}{2}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知集合A={0，1，2}，B={m，3，4}，若A∩B={2}，则实数m=（　　）
    A．4B．3C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．在△ABC 中，∠C=$\frac{2π}{3}$，a=6．
    （Ⅰ）若c=14，求sinA的值；
    （Ⅱ）若△ABC的面积为3$\sqrt{3}$，求c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．函数y=sin（$\frac{π}{3}$-$\frac{1}{2}$x），x∈[-2π，2π]的单调递增区间是（　　）
    A．[-$\frac{π}{3}$，$\frac{5π}{3}$]B．[-2π，-$\frac{π}{3}$]C．[$\frac{5π}{3}$，2π]D．[-2π，-$\frac{π}{3}$]和[$\frac{5π}{3}$，2π]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

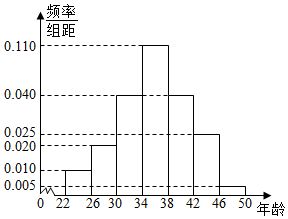    12．2016年1月1日，我国实施“全面二孩”政策，中国社会科学院在某地（已婚男性约15000人）随机抽取了150名已婚男性，其中愿意生育二孩的有100名，经统计，该100名男性的年龄情况对应的频率分布直方图如下；
    （1）求这100名已婚男性的年龄平均值$\overline{x}$和样本方差s2（同组数据用区间的中点值代替，结果精确到个位）；
    （2）（Ⅰ）试估计该地愿意生育二孩的已婚男性人数；
         （Ⅱ）由直方图可以认为，愿意生育二孩的已婚男性的年龄ξ服从正态分布N（μ，δ2），其中μ近似样本的平均值$\overline{x}$，δ2近似为样本的方差s2，试问：该地愿意生育二孩且处于较佳的生育年龄ξ（ξ∈（26，31））的总人数约为多少？（结果精确到个位）
    附：若ξ～N（μ，δ2），则P（μ-δ＜ξ＜μ+δ）=0.6826，P（μ-2δ＜ξ＜μ+2δ）=0.9544．

    查看答案和解析>>

    同步练习册答案