
2013年我国汽车拥有量已超过2亿(目前只有中国和美国超过2亿),为了控制汽车尾气对环境的污染,国家鼓励和补贴购买小排量汽车的消费者,同时在部分地区采取对新车限量上号.某市采取对新车限量上号政策,已知2013年年初汽车拥有量为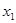 (
(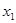 =100万辆),第
=100万辆),第 年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为
年(2013年为第1年,2014年为第2年,依次类推)年初的拥有量记为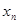 ,该年的增长量
,该年的增长量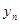 和
和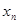 与
与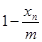 的乘积成正比,比例系数为
的乘积成正比,比例系数为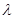
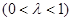 其中
其中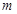 =200万.
=200万.
(1)证明: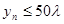 ;
;
(2)用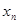 表示
表示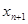 ;并说明该市汽车总拥有量是否能控制在200万辆内.
;并说明该市汽车总拥有量是否能控制在200万辆内.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
设不等式组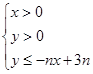 所表示的平面区域为Dn,记Dn内 的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内 的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
(1) 求证:数列{an}的通项公式是an=3n(n∈N*).
(2) 记数列{an}的前n项和为Sn,且Tn=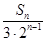 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知各项均为正数的数列{ }满足
}满足 -
-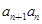 -2
-2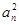 =0,n∈N﹡,且
=0,n∈N﹡,且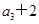 是a2,a4的等差中项.
是a2,a4的等差中项.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若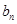 =
=
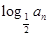 ,
,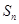 =b1+b2+…+
=b1+b2+…+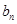 ,求
,求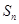 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列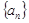 满足
满足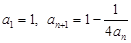 ,其中
,其中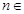 N*.
N*.
(Ⅰ)设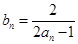 ,求证:数列
,求证:数列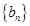 是等差数列,并求出
是等差数列,并求出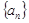 的通项公式
的通项公式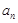 ;
;
(Ⅱ)设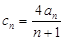 ,数列
,数列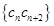 的前
的前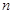 项和为
项和为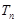 ,是否存在正整数
,是否存在正整数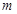 ,使得
,使得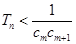 对于
对于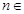 N*恒成立,若存在,求出
N*恒成立,若存在,求出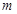 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数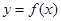 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为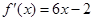 ,数列
,数列 的前
的前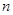 项和为
项和为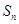 ,点
,点 均在函数
均在函数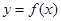 的图像上.
的图像上.
(1)求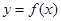 的解析式;
的解析式;
(2)求数列 的通项公式;
的通项公式;
(3)设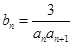 ,
, 是数列
是数列 的前n项和,求使得
的前n项和,求使得 对所有
对所有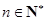 都成立的最小正整数
都成立的最小正整数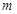 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com