
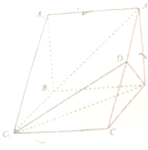
 如图,在四棱锥A-BCDE中,AB=AC=$\frac{\sqrt{2}}{2}$BC,点F为矩形BCDE的对角线的交点,G是AE的中点,平面BCDE⊥平面ABC.
如图,在四棱锥A-BCDE中,AB=AC=$\frac{\sqrt{2}}{2}$BC,点F为矩形BCDE的对角线的交点,G是AE的中点,平面BCDE⊥平面ABC.分析 (1)由已知可得BE⊥面ABC,取BE中点K,连接FK,GK,可证面KFG∥面ABC,从而得到BE⊥面KFG,即FG⊥BE,再由线段AF=FE,G为AE中点得FG⊥AE,然后利用线面垂直的判断得GF⊥平面ABE;
(2)设CD=x,直接由${V}_{A-BCDE}=\frac{1}{3}•4x•2=16$求解x得CD的长.
解答 (1)证明:如图, ∵平面BCDE⊥平面ABC,且BCDE为矩形,
∵平面BCDE⊥平面ABC,且BCDE为矩形,
∴BE⊥面ABC,取BE中点K,连接FK,GK,
∵F为EC的中点,G为AE的中点,
∴KF∥BC,KG∥AB,从而证得面KFG∥面ABC,
∴BE⊥面KFG,则FG⊥BE,
取BC中点H,设BC=$\sqrt{2}a$,则AB=AC=a,
∴三角形BAC为Rt三角形,AH=$\frac{\sqrt{2}}{2}a$,
再设BE=b,则$AF=\sqrt{\frac{{a}^{2}}{2}+\frac{{b}^{2}}{4}}$,EF=$\frac{1}{2}\sqrt{2{a}^{2}+{b}^{2}}=\sqrt{\frac{{a}^{2}}{2}+\frac{{b}^{2}}{4}}$,
∴AF=FE,
又G为AE中点,
∴FG⊥AE,
又AE∩BE=E,
∴GF⊥平面ABE;
(2)解:∵BC=4,
∴AH=$\frac{1}{2}BC=2$,
设CD=x,
则${V}_{A-BCDE}=\frac{1}{3}•4x•2=16$,即x=6.
∴CD的长为6.
点评 本小题主要考查空间线面关系、二面角的度量、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,∠ABC=∠PCA=30°.
如图,在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,∠ABC=∠PCA=30°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC
如图,AB,CD为圆O的两条直径,P为圆O所在平面外的一点,且PA=PB=PC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32$\sqrt{3}$ | B. | $\frac{5\sqrt{3}}{3}$ | C. | 23$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com