
分析 (1)求出f(x)=2sin(2x+$\frac{π}{6}$)+1,由此能求出函数y=f(x)的最小正周期和函数y=f(x)的单调增区间.
(2)由f(A)=2,求出A=$\frac{π}{3}$,由$a=\sqrt{7}$,利用余弦定理得b=2c.由此能求出△ABC的面积.
解答 解:(1)∵$\overrightarrow{a}$=(2cosx,$\sqrt{3}$sin2x),$\overrightarrow{b}$=(cosx,1),x∈R,
∴f(x)=$\overrightarrow{a}$$•\overrightarrow{b}$=$2co{s}^{2}x+\sqrt{3}sin2x$
=$\sqrt{3}sin2x+cos2x+1$=2sin(2x+$\frac{π}{6}$)+1,
∴函数y=f(x)的最小正周期为T=π,
单调递增区间满足-$\frac{π}{2}$+2kπ$≤2x+\frac{π}{6}≤$$\frac{π}{2}$+2kπ,k∈Z.
解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z.
∴函数y=f(x)的单调增区间是[-$\frac{π}{3}$+kπ,$\frac{π}{6}+kπ$],k∈Z.
(2)∵f(A)=2,∴2sin(2A+$\frac{π}{6}$)+1=2,即sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,
又∵0<A<π,∴A=$\frac{π}{3}$,
∵$a=\sqrt{7}$,由余弦定理得a2=b2+c2-2bccosA=(b+c)2-3bc=7,①
∵sinB=2sinC,∴b=2c.②
由①②得c2=$\frac{7}{3}$,∴${S}_{△ABC}=\frac{7\sqrt{3}}{6}$.
点评 本题考查三角函数的最小正周期、单调递增区间的求法,考查三角形面积的求法,考查同角三角函数、三角函数的最小正周期、三角函数的增区间、作弦定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
 如图,若N=10,则输出的数等于( )
如图,若N=10,则输出的数等于( )| A. | $\frac{10}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{10}{11}$ | D. | $\frac{12}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 3 | 4 | 5 | 6 | 7 | 8 | |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 | -3.0 |
| A. | ${\;}_{a}^{∧}$>0,${\;}_{b}^{∧}$>0 | B. | ${\;}_{a}^{∧}$>0,${\;}_{b}^{∧}$<0 | C. | ${\;}_{a}^{∧}$<0,${\;}_{b}^{∧}$>0 | D. | ${\;}_{a}^{∧}$<0,${\;}_{b}^{∧}$<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中,点M、N、P分别在AA1、BC、BB1上运动,且AM=CN=B1P=X(0<X<2).记三棱锥P-MNB1的体积为,V(X)则函数Y=V(X)的图象大致为( )
如图,在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中,点M、N、P分别在AA1、BC、BB1上运动,且AM=CN=B1P=X(0<X<2).记三棱锥P-MNB1的体积为,V(X)则函数Y=V(X)的图象大致为( )| A. |  | B. |  | C. | 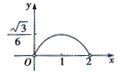 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com