Question

10．在长方体ABCD-A₁B₁C₁D₁中，AB=BC=$\sqrt{2}$AA₁，Q是棱CC₁上的动点，则当BQ+QD₁的长度取得最小值时，直线B₁Q与直线AD所成角的正切值为$\frac{\sqrt{2}}{4}$．

Answer 1

分析 当BQ+D₁Q的长度取得最小值时Q是CC₁的中点，以D₁为原点，D₁A₁为x轴，D₁C₁为y轴，D₁D为z轴，建立空间直角坐标系，利用向量法能求出直线B₁Q和直AD所成的角的正切值．

解答 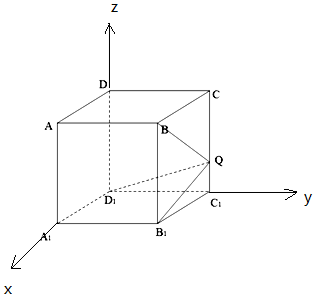解：设AB=BC=$\sqrt{2}$AA₁=$\sqrt{2}$，
把B₁C₁CB展开与D₁C₁CD成一个长方形D₁B₁BD时，
连结D₁B，交CC₁于Q时，当BQ+D₁Q的长度取得最小值，
此时Q是CC₁的中点，
以D₁为原点，D₁A₁为x轴，D₁C₁为y轴，D₁D为z轴，建立空间直角坐标系，
${B}_{1}（\sqrt{2}，\sqrt{2}，0）$，Q（0，$\sqrt{2}$，$\frac{1}{2}$），A（ $\sqrt{2}，0，1）$，D（0，0，1），
$\overrightarrow{AD}=（-\sqrt{2}，0，0）$，$\overrightarrow{{B}_{1}Q}=（-\sqrt{2}，0，\frac{1}{2}）$
cos$＜\overrightarrow{AD}，\overrightarrow{{B}_{1}Q}＞$=$\frac{\overrightarrow{AD}•\overrightarrow{{B}_{1}Q}}{|\overrightarrow{AD}||\overrightarrow{{B}_{1}Q}|}$=$\frac{2}{\sqrt{2}×\frac{3}{2}}=\frac{2\sqrt{2}}{3}$．
设直线B₁Q和直线AD所成角为θ，则cos$θ=\frac{2\sqrt{2}}{3}$，tanθ=$\frac{\sqrt{2}}{4}$
故答案为：$\frac{\sqrt{2}}{4}$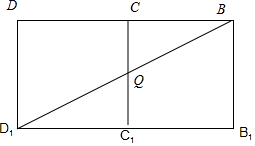

点评 本题考查线线角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．