
【题目】如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD是以AD为底的等腰三角形.
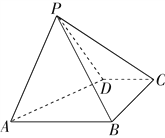
(Ⅰ)证明:AD⊥PB;
(Ⅱ)若四棱锥P-ABCD的体积等于![]() ,平面CMN∥平面PAD,且分别交PB,AB于点M,N,试确定M,N的位置,并求△CMN的面积.
,平面CMN∥平面PAD,且分别交PB,AB于点M,N,试确定M,N的位置,并求△CMN的面积.
【答案】(Ⅰ)见解析(Ⅱ) 见解析
【解析】
试题分析:(1) 取AD的中点G,通过证明AD⊥面PGB,可得AD⊥PB.
(2) 先证明PG⊥底面ABCD,由VP-ABCD=![]() ×PG×
×PG×![]() =
=![]() ,得PG=
,得PG=![]() ,进而求得CN=2,CM=
,进而求得CN=2,CM=![]() ,及S△CMN.
,及S△CMN.
试题解析:(Ⅰ)证明:取AD的中点G,连接PG,GB,
因为PA=PD,
所以PG⊥AD,
因为AB=AD,∠DAB=60°,
所以△DAB是等边三角形,所以BG⊥AD,
又因为PG∩BG=G,PG,BG面PGB,
所以AD⊥面PGB,所以AD⊥PB.
(Ⅱ)解:分别取PB,AB的中点M,N,
则MN∥PA,
因为ABCD是梯形,且DC∥AB,DC=![]() AB,
AB,
所以CD∥AN,DC=AN,于是ANCD为平行四边形,所以CN∥AM,
所以面CMN∥面PAD,
因为侧面PAD⊥底面ABCD,PG⊥AD,
所以PG⊥底面ABCD,
又ABCD的面积为![]() (1+2)×
(1+2)×![]() =
=![]() ,
,
所以VP-ABCD=![]() ×PG×
×PG×![]() =
=![]() ,得PG=
,得PG=![]() ,
,
所以PA=![]() =2,得MN=1,CN=2,
=2,得MN=1,CN=2,
在△PBC和△CBM中,![]() =
=![]() ,
,
所以△PBC∽△CBM,得CM=![]() ,
,
所以△CNM是直角三角形,
S△CMN=![]() ·MN·CM=
·MN·CM=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在坐标原点,焦点F在x轴上,抛物线C上一点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
![]() Ⅰ
Ⅰ![]() 求抛物线C的标准方程;
求抛物线C的标准方程;
![]() Ⅱ
Ⅱ![]() 设点
设点![]() ,过点
,过点![]() 的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为
的直线l与抛物线C相交于A,B两点,记直线MA与直线MB的斜率分别为![]() ,
,![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率与双曲线
的离心率与双曲线![]() 的离心率互为倒数,且过点
的离心率互为倒数,且过点![]() .
.
(1)求椭圆C的方程;
(2)过![]() 作两条直线
作两条直线![]() 与圆
与圆![]() 相切且分别交椭圆于M、N两点.
相切且分别交椭圆于M、N两点.
① 求证:直线MN的斜率为定值;
② 求△MON面积的最大值(其中O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,若
时,若![]() 在区间
在区间![]() 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有实数对![]() :当a是整数时,存在
:当a是整数时,存在![]() ,使得
,使得![]() 是
是![]() 的最大值,
的最大值,![]() 是
是![]() 的最小值;
的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区该农产品的年产量.
附: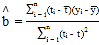 ,
,![]() . 参考数据:
. 参考数据: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1∶3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文、理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.

(1)求a的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的2×2列联表,并判断在犯错误的概率不超过0.05的前提下能否认为“获奖与学生的文、理科有关”.
文科生 | 理科生 | 总计 | |
获奖 | 5 | ||
不获奖 | |||
总计 | 200 |
附表及公式:
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com