
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用导数可以判定其单调性,再判断出奇偶性,即可判断出结论.
解答 解:∵f(x)=x2-2cosx,∴f′(x)=2x+2sinx,
∴当x=0时,f′(0)=0;当x∈[-$\frac{π}{2}$,0)时,f′(x)<0,函数f(x)在此区间上单调递减;
当x∈(0,$\frac{π}{2}$]时,f′(x)>0,函数f(x)在此区间上单调递增.
∴函数f(x)在x=0时取得最小值,f(0)=0-1=-1.
∵x∈[-$\frac{π}{2}$,$\frac{π}{2}$],都有f(-x)=f(x),∴f(x)是偶函数.
根据以上结论可得:
①当x1>x2时,则f(x1)>f(x2)不成立;
②当x12>x22时,得|x1|>|x2|,则f(|x1|)>f(|x2|),f(x1)>f(x2)恒成立;
③当|x1|>x2时,由函数f(x)=x2-2cosx是偶函数,知f(x1)=f(|x1|)>f(x2)不恒成立;
④x1>|x2|时,则f(x1)>f(|x2|)=f(x2)恒成立.
综上可知:能使f(x1)>f(x2)恒成立的有②④.
故选:B.
点评 本题考查命题真假的判断,是中档题,熟练掌握利用导数研究函数的单调性、判定函数的奇偶性等是解题的关键.


科目:高中数学 来源: 题型:解答题
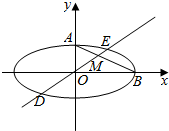 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l3⊥l4 | B. | l3∥l4 | ||
| C. | l3,l4既不平行也不垂直 | D. | l3,l4的位置关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
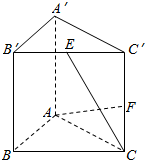 在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )
在直三棱柱ABC-A′B′C′中,AB=AC=2,AA′=3,AB⊥AC,E为棱B′C′的中点,F为侧棱CC′上一点,若CE⊥AF,则AF与平面ABB′A′所成的角的正切值为( )| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com