
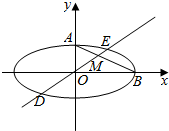
 ��ͼ����ƽ��ֱ������ϵxOy�У���ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����A��B�ֱ�Ϊ��ԲC���϶��㡢�Ҷ��㣬������ԭ���ֱ�߽���ԲC��D��E���㣬��AB��M�㣬���е�E�ڵ�һ���ޣ���ֱ��DE��б��Ϊk��
��ͼ����ƽ��ֱ������ϵxOy�У���ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$����A��B�ֱ�Ϊ��ԲC���϶��㡢�Ҷ��㣬������ԭ���ֱ�߽���ԲC��D��E���㣬��AB��M�㣬���е�E�ڵ�һ���ޣ���ֱ��DE��б��Ϊk������ ��1��ͨ�������ʵ�ֵ��a��b��c����֮��Ĺ�ϵ����ɵ�a=2b����������ͨ����A��0��b����B��2b��0�������ù�ԭ�㼰AB�е�P��ֱ��б��Ϊ$\frac{1}{2}$�ɵý��ۣ�
��2����ͨ����A���꼰�����ʿ�֪��Բ�ķ��̣������ɵ�A��B�����꣬ͨ����ֱ��AB��DE�ķ��̼�M��D��E�ı�������S��ADM=6S��AEM����M��AB�ϵó�һ������k�ķ��̣���������ɵý��ۣ���ͨ���ı���ADBE���ΪS=S��OAD+S��OAE+S��ODB+S��OEB���������ݻ�������ʽ������������ֵ��
���  �⣺��1����e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$��
�⣺��1����e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$=$\frac{\sqrt{3}}{2}$��
��$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{3}{4}$����$\frac{b}{a}$=$\frac{1}{2}$��
����ԲC��$\frac{{x}^{2}}{4{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��
��A��0��b����B��2b��0������AB�е�P��b��$\frac{1}{2}$b����
��kOP=$\frac{\frac{1}{2}b-0}{b-0}$=$\frac{1}{2}$����ֱ��DE��б��k=$\frac{1}{2}$��
���P���M�غϣ���ֱ��DEƽ���߶�AB��
��2���ɵ�A��0��1����֪b=1��
��e2=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}$=$\frac{{a}^{2}-1}{{a}^{2}}$=$\frac{3}{4}$����֪a2=4��
����ԲC��$\frac{{x}^{2}}{4}$+y2=1������B��2��0����
ֱ��AB��DE�ķ��̷ֱ�Ϊx+2y=2��y=kx��k��0����
����ͼ����M��x0��kx0����D��x1��kx1����E��x2��kx2��������x1��x2��
��x1��x2���㷽�̣�1+4k2��x2=4��
��x2=-x1=$\frac{2}{\sqrt{1+4{k}^{2}}}$����
��S��ADM=6S��AEM��
��x0-x1=6��x2-x0������x0=$\frac{1}{7}$��6x2+x1��=$\frac{5}{7}$x2=$\frac{10}{7\sqrt{1+4{k}^{2}}}$��
�֡���M��AB�ϣ�
��x0+2kx0=2����x0=$\frac{2}{1+2k}$��
����$\frac{10}{7\sqrt{1+4{k}^{2}}}$=$\frac{2}{1+2k}$�������24k2-25k+6=0��
���k=$\frac{2}{3}$��k=$\frac{3}{8}$��
���������֪|AO|=1��|BO|=2��D��x1��kx1����E��x2��kx2����
������y1=kx1��y2=kx2��
�ɢٿ�֪��x2��0������E��D����ԭ��Գƿ�֪y2=-y1��0��
���ı���ADBE���S=S��OAD+S��OAE+S��ODB+S��OEB
=$\frac{1}{2}$|OA|•��-x1��+$\frac{1}{2}$|OA|•x2+$\frac{1}{2}$|OB|•y2+$\frac{1}{2}$|OB|•��-y1��
=$\frac{1}{2}$|OA|��x2-x1��+$\frac{1}{2}$|OB|��y2-y1��
=x2+2y2
=$\sqrt{��{x}_{2}+2{y}_{2}��^{2}}$
=$\sqrt{{{x}_{2}}^{2}+4{{y}_{2}}^{2}+4{x}_{2}{y}_{2}}$
��$\sqrt{2��{{x}_{2}}^{2}+4{{y}_{2}}^{2}��}$
=2$\sqrt{2}$��
���ҽ���x2=2y2ʱ����ʽȡ�Ⱥţ�
�����ı���ADBE���S�����ֵΪ2$\sqrt{2}$��
���� ������Ҫ������ֱ������Բ���ۺ����⣬ֱ����Բ���ߵ��ۺ�������֧��Բ����֪ʶ��ϵ���ص����ݣ�����Ľ��������ڿ��������������ȣ�����ͬ�Ľ���;����������������ܴ�ע����ⷽ���Ļ��ۣ��������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
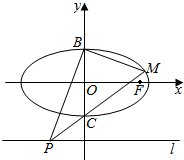 ��ͼ����֪��ԲO��$\frac{{x}^{2}}{4}$+y2=1���ҽ���ΪF����B��C�ֱ�����ԲO���ϡ��¶��㣬��P��ֱ��l��y=-2�ϵ�һ�����㣨��y�ύ����⣩��ֱ��PC����Բ����һ��M��
��ͼ����֪��ԲO��$\frac{{x}^{2}}{4}$+y2=1���ҽ���ΪF����B��C�ֱ�����ԲO���ϡ��¶��㣬��P��ֱ��l��y=-2�ϵ�һ�����㣨��y�ύ����⣩��ֱ��PC����Բ����һ��M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��x��2 | B�� | 1��x��3 | C�� | 0��x��3 | D�� | 1��x��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
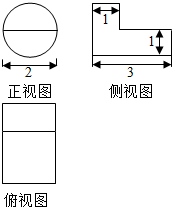
| A�� | 6��+4 | B�� | ��+4 | C�� | $\frac{5��}{2}$ | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com