
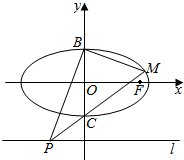
 如图,已知椭圆O:$\frac{{x}^{2}}{4}$+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.
如图,已知椭圆O:$\frac{{x}^{2}}{4}$+y2=1的右焦点为F,点B,C分别是椭圆O的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.分析 (1)求得椭圆的a,b,c,可得B,C,F的坐标,求得PM的方程代入椭圆方程,可得M,再由BF的方程,求得M到直线BF的距离,再由三角形的面积公式计算即可得到所求值;
(2)①设P(m,-2)(m≠0),求得PM的方程,代入椭圆方程求得M的坐标,运用直线的斜率公式计算即可得到k1•k2为定值;
②求得向量PB,PM的坐标,运用向量的数量积的坐标表示,可得$\overrightarrow{PB}$•$\overrightarrow{PM}$=$\frac{{m}^{4}+15{m}^{2}+36}{4+{m}^{2}}$,令t=4+m2>4,由函数的单调性,可得所求范围.
解答 解:(1)由椭圆的方程$\frac{{x}^{2}}{4}$+y2=1,可得a=2,b=1,c=$\sqrt{3}$,
即有B(0,1),C(0,-1),F($\sqrt{3}$,0),
直线PM:$\frac{x}{\sqrt{3}}$+$\frac{y}{-1}$=1,即为y=$\frac{\sqrt{3}}{3}$x-1,
代入椭圆方程可得,M($\frac{8\sqrt{3}}{7}$,$\frac{1}{7}$),
连接BF,可得BF:$\frac{x}{\sqrt{3}}$+y=1,即为x+$\sqrt{3}$y-$\sqrt{3}$=0,
而BF=a=2,M到直线BF的距离为d=$\frac{|\frac{8\sqrt{3}}{7}+\frac{\sqrt{3}}{7}-\sqrt{3}|}{\sqrt{1+3}}$=$\frac{\sqrt{3}}{7}$,
即有S△MBF=$\frac{1}{2}$BF•d=$\frac{1}{2}$•2•$\frac{\sqrt{3}}{7}$=$\frac{\sqrt{3}}{7}$;
(2)①设P(m,-2)(m≠0),kPM=$\frac{-1-(-2)}{0-m}$=-$\frac{1}{m}$,
PM:y=-$\frac{1}{m}$x-1,代入椭圆方程可得(4+m2)x2+8mx=0,
解得M(-$\frac{8m}{4+{m}^{2}}$,$\frac{4-{m}^{2}}{4+{m}^{2}}$),k1=$\frac{\frac{4-{m}^{2}}{4+{m}^{2}}-1}{-\frac{8m}{4+{m}^{2}}}$=$\frac{1}{4}$m,k2=$\frac{1-(-2)}{0-m}$=-$\frac{3}{m}$,
则k1k2=$\frac{1}{4}$m•(-$\frac{3}{m}$)=-$\frac{3}{4}$为定值;
②由①知,$\overrightarrow{PB}$=(-m,3),$\overrightarrow{PM}$=(-$\frac{8m}{4+{m}^{2}}$-m,$\frac{4-{m}^{2}}{4+{m}^{2}}$+2)=(-$\frac{{m}^{3}+12m}{4+{m}^{2}}$,$\frac{{m}^{2}+12}{4+{m}^{2}}$),
$\overrightarrow{PB}$•$\overrightarrow{PM}$=-m•(-$\frac{{m}^{3}+12m}{4+{m}^{2}}$)+3•$\frac{{m}^{2}+12}{4+{m}^{2}}$=$\frac{{m}^{4}+15{m}^{2}+36}{4+{m}^{2}}$,
令t=4+m2>4,即有$\overrightarrow{PB}$•$\overrightarrow{PM}$=$\frac{(t-4)^{2}+15(t-4)+36}{t}$=t-$\frac{8}{t}$+7,
由y=t-$\frac{8}{t}$+7在(4,+∞)单调递增,则$\overrightarrow{PB}$•$\overrightarrow{PM}$=t-$\frac{8}{t}$+7>4-$\frac{8}{4}$+7=9,
故$\overrightarrow{PB}$•$\overrightarrow{PM}$的取值范围为(9,+∞).
点评 本题考查椭圆的方程和性质及运用,考查直线和椭圆方程联立求交点,同时考查向量的数量积的坐标表示和直线的斜率公式和直线方程的运用,考查运算能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 最大角为120°的钝角三角形 | D. | 最大角小于120°的钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (1,3] | C. | [2,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{39}$ | B. | 6$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
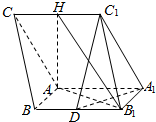 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥侧面ABB1A1,AC=AA1=$\sqrt{2}$AB,∠AA1C1=60°.AB⊥AA1,H为棱CC1的中点,D为BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
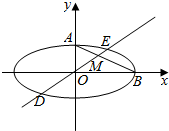 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,点A,B分别为椭圆C的上顶点、右顶点,过坐标原点胡直线交椭圆C于D,E两点,交AB于M点,其中点E在第一象限,设直线DE的斜率为k.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com