练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设
    e1
    ，
    e2
    是平面内一组基底，证明：当λ1
    e1
    +λ2
    e2
    =0时，恒有λ1=λ2=0成立．
    考点：平面的基本性质及推论
    专题：平面向量及应用
    分析：利用反证明法证明．
    解答： 证明：∵
    e1
    ，
    e2
    是平面内一组基底，∴
    e1
    ，
    e2
    不共线，
    假设λ1≠λ2≠0，
    由题干得：
    e1
    =-（
    λ2
    λ1
    ）
    e2
    ，∴
    e1
    ，
    e2
    共线，
    与已知条件矛盾，
    ∴假设不成立，
    ∴当λ1
    e1
    +λ2
    e2
    =0时，恒有λ1=λ2=0成立．
    点评：本题考查两实数同时等于0的证明，解题时要认真审题，要注意向量知识的灵活运用，是基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若直线l不平行于平面 α，且l?α，则（　　）
    A、α内不存在与l平行的直线
    B、α内的所有直线与l异面
    C、α内存在唯一的直线与l平行
    D、α内的直线与l都相交

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设f（x）=x2-（k+1）x+k
    （1）若关于x的不等式f（x）＜0为（1，2），求实数k的值；
    （2）设k＞1且k≠2，求关于x的不等式
    f(x)
    2-x
    ＜0的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

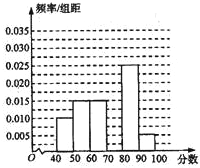    某校高一年级有2000名学生，从中随机抽出60名学生，将这60名学生的某次数学考试成绩（百分制）分成六段[40，50），[50，60），…，[90，100]后，得到如图所示的频率分布直方图，观察图形的信息，回答下列问题：
    （1）求分数在[70，80）内的频率，并补全这个频率分布直方图；
    （2）根据频率分布直方图推测，高一年级2000名学生在该次数学考试中成绩低于60分的人数；
    （3）统计方法中，同一组数据常用该组区间的中点值作为代表，请根据频率分布直方图估计高一年级该次数学考试的平均成绩．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，角A，B，C所对的边分别a，b，c，且
    sinC
    2sinA-sinC
    =
    ccosB
    bcosC
    ．
    （Ⅰ）求角B的大小；
    （Ⅱ）若线段AB的中点为D，且a=1，CD=
    		3
    ，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=（x2+ax+a）ex（e为自然对数的底数）．
    （1）若a=-1，求函数f（x）的单调区间；
    （2）是否存在实数a，使函数f（x）在R上是单调增函数？若存在，求出a的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

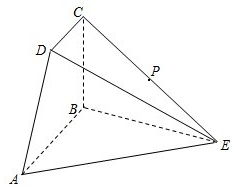    如图所示，四边形ABCD为直角梯形，AB∥CD，AB⊥BC，△ABE为等边三角形，且平面ABCD⊥平面ABE，AB=2CD=2BC=2，P为CE中点．
    （Ⅰ）求证：AB⊥DE；
    （Ⅱ）求平面ADE与平面BCE所成的锐二面角的余弦值；
    （Ⅲ）在△ABE内是否存在一点Q，使PQ⊥平面CDE，如果存在，求PQ的长；如果不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知偶函数f（x）在[0，+∞）上单调递减，f（2）=0，则满足不等式f（x）＞0的实数x的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，角A，B，C所对的边分别为a，b，c，若B=60°，b=
    		3
    ，则a+c的最大值为
     
    ．

    查看答案和解析>>

    同步练习册答案