
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 建立坐标系,根据$\overrightarrow{AF}$$•\overrightarrow{DE}$=-4求出E点坐标,再计算$\overrightarrow{AE}•\overrightarrow{BF}$.
解答 解:以A为原点,以AD、AB为坐标轴建立坐标系,如图所示: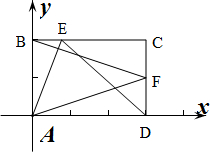
则A(0,0),B(0,2),C(3,2),D(3,0),F(3,1),
设E(a,2),则$\overrightarrow{AF}$=(3,1),$\overrightarrow{DE}$=(a-3,2),$\overrightarrow{AE}$=(a,2),$\overrightarrow{BF}$=(3,-1),
∴$\overrightarrow{AF}•\overrightarrow{DE}$=3(a-3)+2=-4,解得a=1,
∴$\overrightarrow{AE}•\overrightarrow{BF}$=3a-2=1.
故选B.
点评 本题考查了平面向量的数量积运算,建立坐标系转化为坐标运算可简化计算,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | -15 | C. | 5 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
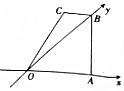 用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形,其中梯形的上底是下底的$\frac{1}{2}$,若原平面图形的面积为3$\sqrt{2}$,则OA的长为( )
用斜二测画法得到一个水平放置的平面图形的直观图为如图所示的直角梯形,其中梯形的上底是下底的$\frac{1}{2}$,若原平面图形的面积为3$\sqrt{2}$,则OA的长为( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
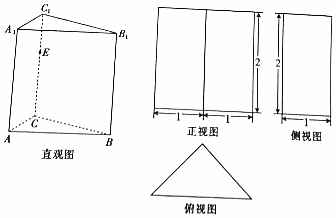
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com