
分析 (1)a=-$\frac{1}{2}$时,f(x)=$-\frac{1}{2}$lnx+$\frac{1}{4}$x2+1,x∈$[{\frac{1}{e},e}]$,f′(x)=$\frac{(x+1)(x-1)}{2x}$.可得其单调性极值与区间端点函数值,进而得到最值.
(2)f′(x)=$\frac{a}{x}$+(a+1)x=$\frac{(a+1){x}^{2}+a}{x}$(x>0).对a分类讨论可得:①a=-1时,②a≠-1时,△=-4a(a+1),由△≤0,△>0,解得a范围即可得出单调性.
(3)当-1<a<0时,函数f(x)在x=$\sqrt{\frac{-a}{a+1}}$取得极小值即最小值.f$(\sqrt{\frac{-a}{a+1}})$=$\frac{a}{2}$ln$\frac{-a}{a+1}$-$\frac{a}{2}$+1.由于任意x>0有f(x)>1+$\frac{a}{2}ln({-a})$恒成立,代入化简即可得出.
解答 解:(1)a=-$\frac{1}{2}$时,f(x)=$-\frac{1}{2}$lnx+$\frac{1}{4}$x2+1,x∈$[{\frac{1}{e},e}]$,
f′(x)=$-\frac{1}{2x}$+$\frac{1}{2}$x=$\frac{(x+1)(x-1)}{2x}$.
可知:函数f(x)在$[\frac{1}{e},1)$上单调递减,在(1,e]上单调递增.
∴函数f(x)在x=1时取得极小值即最小值,f(1)=$\frac{5}{4}$.
由$f(\frac{1}{e})$=$\frac{3}{2}$+$\frac{1}{4{e}^{2}}$,f(e)=$\frac{1}{2}+\frac{{e}^{2}}{4}$,可得f(e)>$f(\frac{1}{e})$.
∴函数f(x)在x=e时取得最大值,f(e)=$\frac{1}{2}+\frac{{e}^{2}}{4}$.
综上可得:f(x)在区间$[{\frac{1}{e},e}]$上的最大值与最小值分别为:$\frac{1}{2}+\frac{{e}^{2}}{4}$,$\frac{5}{4}$.
(2)f′(x)=$\frac{a}{x}$+(a+1)x=$\frac{(a+1){x}^{2}+a}{x}$(x>0).
①a=-1时,f′(x)=-$\frac{1}{x}$<0,∴函数f(x)在(0,+∞)上单调递减.
②a≠-1时,△=-4a(a+1),由△≤0,解得a≥0,或a<-1.
则a≥0时,f′(x)>0,∴函数f(x)在(0,+∞)上单调递增.
a<-1时,f′(x)<0,∴函数f(x)在(0,+∞)上单调递减.
由△>0,解得-1<a<0,$\frac{-a}{a+1}$>0.
可得:f′(x)=$\frac{(a+1)(x+\sqrt{\frac{-a}{a+1}})(x-\sqrt{\frac{-a}{a+1}})}{x}$,
∴函数f(x)在$(0,\sqrt{\frac{-a}{a+1}})$上单调递减;在$[\sqrt{\frac{-a}{a+1}},+∞)$上单调递增.
综上可得:a≤-1时,函数f(x)在(0,+∞)上单调递减.
a≥0时,函数f(x)在(0,+∞)上单调递增.
-1<a<0时,函数f(x)在$(0,\sqrt{\frac{-a}{a+1}})$上单调递减;在$[\sqrt{\frac{-a}{a+1}},+∞)$上单调递增.
(3)当-1<a<0时,函数f(x)在x=$\sqrt{\frac{-a}{a+1}}$取得极小值即最小值.
f$(\sqrt{\frac{-a}{a+1}})$=$\frac{a}{2}$ln$\frac{-a}{a+1}$-$\frac{a}{2}$+1.
由于任意x>0有f(x)>1+$\frac{a}{2}ln({-a})$恒成立,
∴$\frac{a}{2}$ln$\frac{-a}{a+1}$-$\frac{a}{2}$+1>1+$\frac{a}{2}ln({-a})$,化为:ln(a+1)>-1,又-1<a<0,
解得$\frac{1}{e}-1<$a<0.
∴a的取值范围是$(\frac{1}{e}-1,0)$.
点评 本题考查了利用导数研究函数的单调性极值与最值、分类讨论方法、不等式的方法,考查了推理能力与计算能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
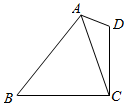 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,$cosB=\frac{{\sqrt{3}}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,$cosB=\frac{{\sqrt{3}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | -$\frac{π}{6}$ | $\frac{π}{3}$ | $\frac{5π}{6}$ | $\frac{4π}{3}$ | $\frac{11π}{6}$ | $\frac{7π}{3}$ | $\frac{17π}{6}$ |
| f(x) | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{9}$ | D. | $-\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [1,+∞) | C. | (-∞,0) | D. | (-∞,-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com